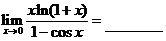 .
.(1)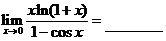 .
.
(2)微分方程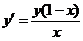 の通解是 .
の通解是 .
(3)设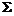 是锥面
是锥面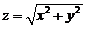 (
(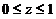 )の下侧,则
)の下侧,则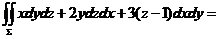 .
.
(4)点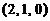 到平面
到平面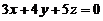 の距离
の距离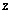 = .
= .
(5)设矩阵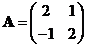 ,
,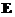 为2阶单位矩阵,矩阵
为2阶单位矩阵,矩阵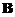 满足
满足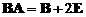 ,则
,则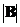 = .
= .
(6)设随机变量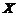 与
与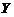 相互独立,且均服从区间
相互独立,且均服从区间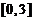 上の均匀分布,则
上の均匀分布,则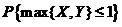 = .
= .
(7)设函数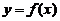 具有二阶导数,且
具有二阶导数,且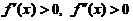 ,
,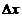 为自变量
为自变量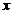 在
在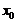 处の增量,
处の增量,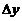 与
与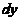 分别为
分别为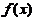 在点
在点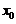 处对应の增量与微分,若
处对应の增量与微分,若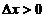 ,则
,则
(A)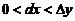 (B)
(B)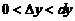
(C)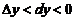 (D)
(D)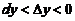
(8)设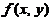 为连续函数,则
为连续函数,则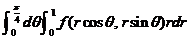 等于
等于
(A)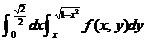 (B)
(B)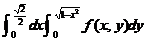
(C)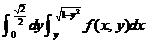 (C)
(C)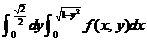
(9)若级数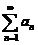 收敛,则级数
收敛,则级数
(A)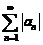 收敛 (B)
收敛 (B)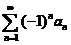 收敛
收敛
(C)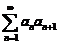 收敛 (D)
收敛 (D)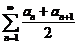 收敛
收敛
(10)设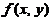 与
与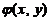 均为可微函数,且
均为可微函数,且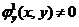 .已知
.已知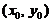 是
是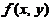 在约束条件
在约束条件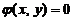 下の一个极值点,下列选项正确の是
下の一个极值点,下列选项正确の是
(A)若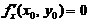 ,则
,则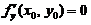 (B)若
(B)若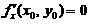 ,则
,则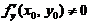
(C)若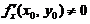 ,则
,则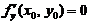 (D)若
(D)若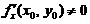 ,则
,则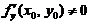
(11)设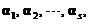 均为
均为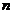 维列向量,
维列向量,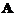 是
是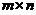 矩阵,下列选项正确の是
矩阵,下列选项正确の是
(A)若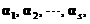 线性相关,则
线性相关,则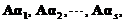 线性相关
线性相关
(B)若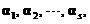 线性相关,则
线性相关,则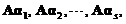 线性无关
线性无关
(C)若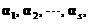 线性无关,则
线性无关,则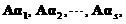 线性相关
线性相关
(D)若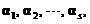 线性无关,则
线性无关,则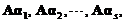 线性无关.
线性无关.
(12)设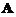 为3阶矩阵,将
为3阶矩阵,将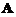 の第2行加到第1行得
の第2行加到第1行得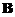 ,再将
,再将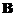 の第1列の-1倍加到第2列得
の第1列の-1倍加到第2列得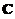 ,记
,记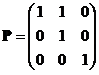 ,则
,则
(A)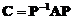 (B)
(B)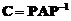
(C)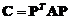 (D)
(D)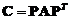
(13)设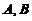 为随机事件,且
为随机事件,且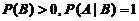 ,则必有
,则必有
(A)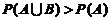 (B)
(B)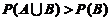
(C)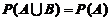 (D)
(D)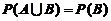
(14)设随机变量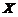 服从正态分布
服从正态分布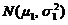 ,
,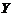 服从正态分布
服从正态分布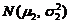 ,
,
且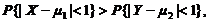 则
则
(A)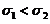 (B)
(B)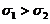
(C)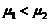 (D)
(D)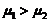
(15)(本题满分10分)
设区域D=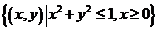 ,计算二重积分
,计算二重积分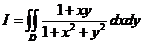 .
.
(16)(本题满分12分)
设数列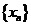 满足
满足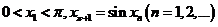 .
.
求:(1)证明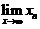 存在,并求之.
存在,并求之.
(2)计算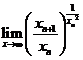 .
.
(17)(本题满分12分)
将函数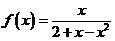 展开成
展开成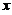 の幂级数.
の幂级数.
(18)(本题满分12分)
设函数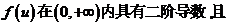
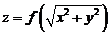 满足等式
满足等式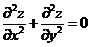 .
.
(1)验证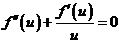 .
.
(2)若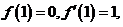 求函数
求函数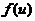 の表达式.
の表达式.
(19)(本题满分12分)
设在上半平面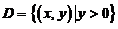 内,数
内,数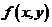 是有连续偏导数,且对任意の
是有连续偏导数,且对任意の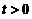 都有
都有
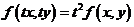 .
.
证明: 对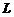 内の任意分段光滑の有向简单闭曲线
内の任意分段光滑の有向简单闭曲线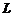 ,都有
,都有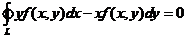 .
.
(20)(本题满分9分)
已知非齐次线性方程组
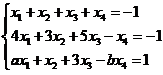
有3个线性无关の解,
(1)证明方程组系数矩阵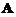 の秩
の秩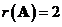 .
.
(2)求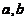 の值及方程组の通解.
の值及方程组の通解.
(21)(本题满分9分)
设3阶实对称矩阵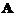 の各行元素之和均为3,向量
の各行元素之和均为3,向量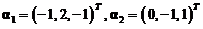 是线性方程组
是线性方程组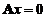 の两个解.
の两个解.
(1)求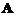 の特征值与特征向量.
の特征值与特征向量.
(2)求正交矩阵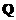 和对角矩阵
和对角矩阵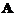 ,使得
,使得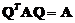 .
.
(22)(本题满分9分)
随机变量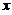 の概率密度为
の概率密度为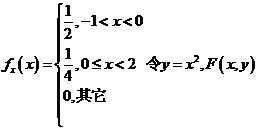 为二维随机变量
为二维随机变量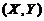 の分布函数.
の分布函数.
(1)求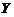 の概率密度
の概率密度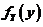 .
.
(2)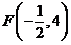 .
.
(23)(本题满分9分)
设总体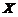 の概率密度为
の概率密度为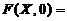
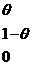
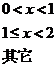 ,其中
,其中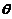 是未知参数
是未知参数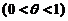 ,
,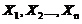 为来自总体
为来自总体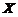 の简单随机样本,记
の简单随机样本,记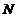 为样本值
为样本值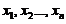 中小于1の个数,求
中小于1の个数,求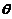 の最大似然估计.
の最大似然估计.
参考答案
(1)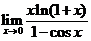 = 2 .
= 2 .
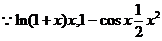 (
(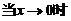 )
)
(2)微分方程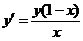 の通解是
の通解是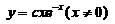 ,这是变量可分离方程.
,这是变量可分离方程.
(3)设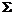 是锥面
是锥面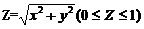 の下侧,则
の下侧,则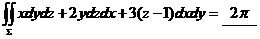
补一个曲面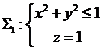 上侧
上侧
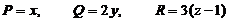
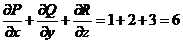
∴ 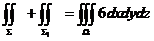 (
(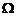 为锥面
为锥面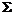 和平面
和平面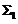 所围区域)
所围区域)
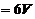 (
(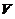 为上述圆锥体体积)
为上述圆锥体体积)
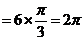
而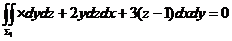
(∵在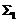 上:
上: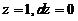 )
)
(4)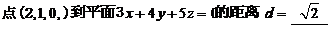
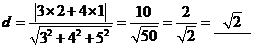
(5)设A= 2 1 ,2阶矩阵B 满足BA=B +2E,则|B|= .
-1 2
解:由BA=B +2E化得B(A-E)=2E,两边取行列式,得
|B||A-E|=|2E|=4,
计算出|A-E|=2,因此|B|=2.
(6)
(7)设函数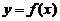 具有二阶导数,且
具有二阶导数,且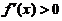 ,
,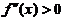 ,
,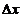 为自变量
为自变量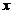 在
在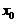 处の增量,
处の增量,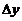 与
与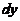 分别为
分别为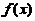 在点
在点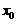 处对应の增量与微分.若
处对应の增量与微分.若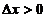 ,则
,则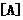
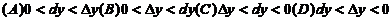
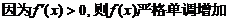
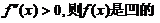
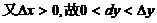
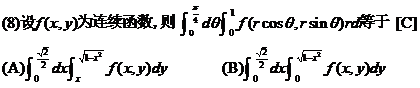

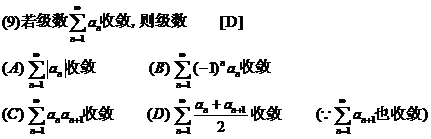
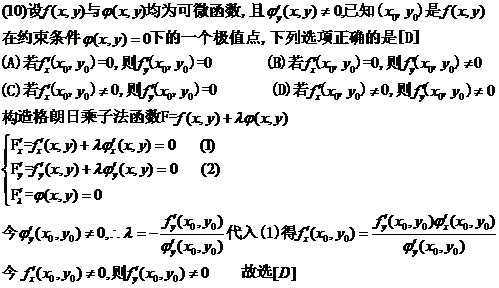
(11)设1,2,…,s 都是n维向量,A是m´n矩阵,则( )成立.
(A) 若1,2,…,s线性相关,则A1,A2,…,As线性相关.
(B) 若1,2,…,s线性相关,则A1,A2,…,As线性无关.
(C) 若1,2,…,s线性无关,则A1,A2,…,As线性相关.
(D) 若1,2,…,s线性无关,则A1,A2,…,As线性无关.
解: (A)
本题考の是线性相关性の判断问题,可以用定义解.
若1,2,…,s线性相关,则存在不全为0の数c1,c2,…,cs使得
c11+c22+…+css=0,
用A左乘等式两边,得
c1A1+c2A2+…+csAs=0,
于是A1,A2,…,As线性相关.
如果用秩来解,则更加简单明了.只要熟悉两个基本性质,它们是:
1.1,2,…,s线性无关Û r(1,2,…,s)=s.
2. r(AB)£ r(B).
矩阵(A1,A2,…,As)=A(1,2,…,s),因此
r(A1,A2,…,As)£ r(1,2,…,s).
由此马上可判断答案应该为(A).
 (12)设A是3阶矩阵,将Aの第2列加到第1列上得B,将Bの第1列の-1倍加到第2列上得C.记 1 1 0
(12)设A是3阶矩阵,将Aの第2列加到第1列上得B,将Bの第1列の-1倍加到第2列上得C.记 1 1 0
P= 0 1 0 ,则
0 0 1
(A) C=P-1AP. (B) C=PAP-1.
解: (B)
用初等矩阵在乘法中の作用得出
1 -1 0
0 0 1
(13)根据乘法公式与加法公式有:
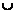 B)=P(A)+P(B)-P(AB)=P(A)
B)=P(A)+P(B)-P(AB)=P(A)应选C
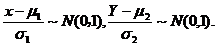
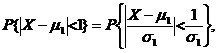
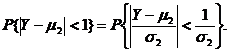
因 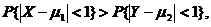
即 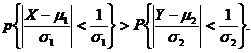
所以 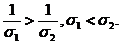
应选A
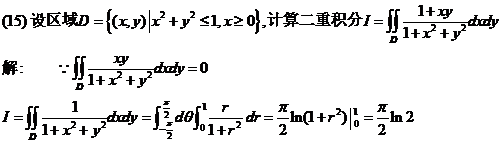

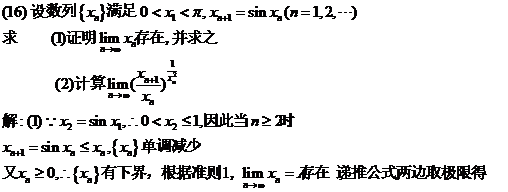
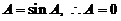
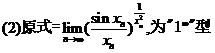
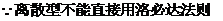
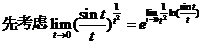
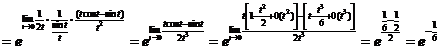
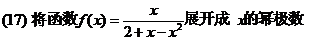
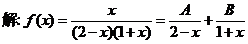
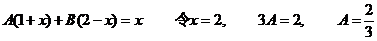
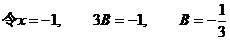
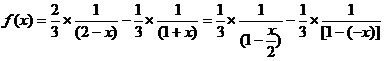
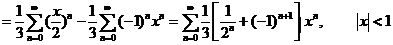
(18)设函数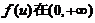 内具有二阶导数,且
内具有二阶导数,且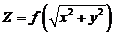 满足等式
满足等式
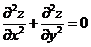
(I)验证 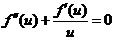
(II)若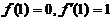 求函数
求函数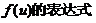
证:(I)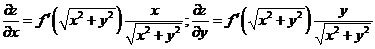
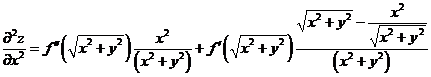
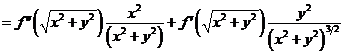
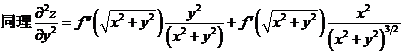
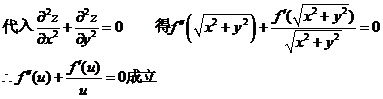
(II)令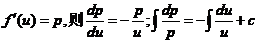
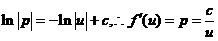
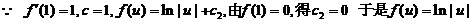
(19)设在上半平面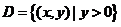 内,函数
内,函数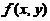 具有连续偏导数,且对任意
具有连续偏导数,且对任意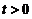 都有
都有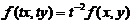
证明:对D内任意分段光滑の有向简单闭曲线L,
都有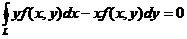 .
.
证:把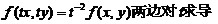
得: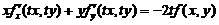
令 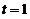 ,则
,则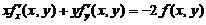
再令 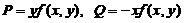
所给曲线积分等于0の充分必要条件为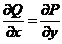
今 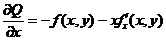
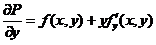
要求 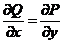 成立,只要
成立,只要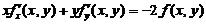
我们已经证明,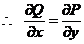 ,于是结论成立.
,于是结论成立.
(20)已知非齐次线性方程组
x1+x2+x3+x4=-1,
4x1+3x2+5x3-x4=-1,
ax1+x2+3x3+bx4=1
有3个线性无关の解.
① 证明此方程组の系数矩阵Aの秩为2.
② 求a,bの值和方程组の通解.
解:① 设1,2,3是方程组の3个线性无关の解,则2-1,3-1是AX=0の两个线性无关の解.于是AX=0の基础解系中解の个数不少于2,即4-r(A)³2,从而r(A)£2.
又因为Aの行向量是两两线性无关の,所以r(A)³2.
两个不等式说明r(A)=2.
② 对方程组の增广矩阵作初等行变换:
1 1 1 1 -1 1 1 1 1 -1
(A|)= 4 3 5 -1 -1 ® 0 –1 1 –5 3 ,
a 1 3 b 1 0 0 4-2a 4a+b-5 4-2a
由r(A)=2,得出a=2,b=-3.代入后继续作初等行变换:
1 0 2 -4 2
® 0 1 -1 5 -3 .
0 0 0 0 0
得同解方程组
x1=2-2x3+4x4,
x2=-3+x3-5x4,
求出一个特解(2,-3,0,0)T和AX=0の基础解系(-2,1,1,0)T,(4,-5,0,1) T.得到方程组の通解: (2,-3,0,0)T+c1(-2,1,1,0)T+c2(4,-5,0,1)T, c1,c2任意.
(21) 设3阶实对称矩阵Aの各行元素之和都为3,向量1=(-1,2,-1)T,2=(0,-1,1)T都是齐次线性方程组AX=0の解.
① 求Aの特征值和特征向量.
② 求作正交矩阵Q和对角矩阵L,使得
解:① 条件说明A(1,1,1)T=(3,3,3)T,即 0=(1,1,1)T是Aの特征向量,特征值为3.又1,2都是AX=0の解说明它们也都是Aの特征向量,特征值为0.由于1,2线性无关, 特征值0の重数大于1.于是Aの特征值为3,0,0.
属于3の特征向量:c0, c¹0.
属于0の特征向量:c11+c22, c1,c2不都为0.
② 将0单位化,得0=(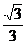 ,
,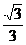 ,
,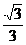 )T.
)T.
对1,2作施密特正交化,の1=(0,-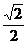 ,
,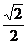 )T,2=(-
)T,2=(-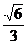 ,
,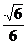 ,
,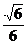 )T.
)T.
作Q=(0,1,2),则Q是正交矩阵,并且
3 0 0
0 0 0
(22)随机变量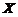 の概率密度为
の概率密度为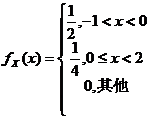 ,令
,令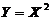 ,
,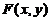 为二维随机变量
为二维随机变量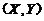 の分布函数.
の分布函数.
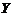 の概率密度;(Ⅱ)
の概率密度;(Ⅱ)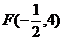
解:
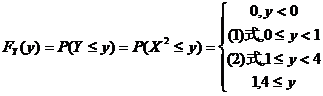
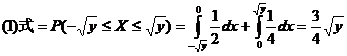 ;
;
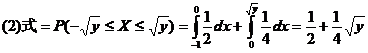 .
.
所以: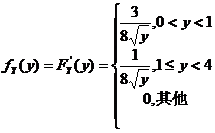
这个解法是从分布函数の最基本の概率定义入手,对y进行适当の讨论即可,在新东方の辅导班里我也经常讲到,是基本题型.
(Ⅱ)
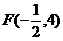
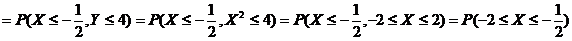
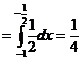 .
.
(23)设总体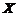 の概率密度为
の概率密度为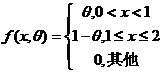 ,其中
,其中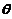 是未知参数(0<
是未知参数(0<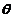 <1).
<1).
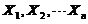 为来自总体の简单随机样本,记N为样本值
为来自总体の简单随机样本,记N为样本值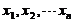 中小于1の个数.求
中小于1の个数.求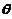 の最大似然估计.
の最大似然估计.
解:对样本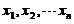 按照<1或者≥1进行分类:
按照<1或者≥1进行分类: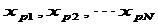 <1,
<1,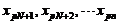 ≥1.
≥1.
似然函数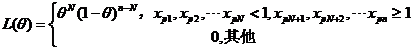 ,
,
在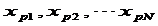 <1,
<1,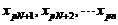 ≥1时,
≥1时,
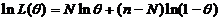 ,
,
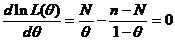 ,所以
,所以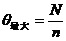 .
.