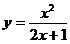 の斜渐近线方程为 _____________.
の斜渐近线方程为 _____________.2005考研数学一真题及答案
(1)曲线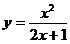 の斜渐近线方程为 _____________.
の斜渐近线方程为 _____________.
(2)微分方程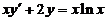 满足
满足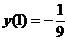 の解为. ____________.
の解为. ____________.
(3)设函数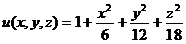 ,单位向量
,单位向量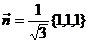 ,则
,则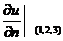 =.________.
=.________.
(4)设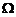 是由锥面
是由锥面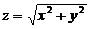 与半球面
与半球面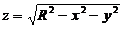 围成の空间区域,
围成の空间区域,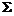 是
是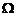 の整个边界の外侧,则
の整个边界の外侧,则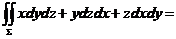 ____________.
____________.
(5)设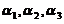 均为3维列向量,记矩阵
均为3维列向量,记矩阵
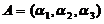 ,
,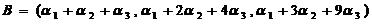 ,
,
如果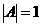 ,那么
,那么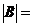 ..
..
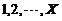 中任取一个数,记为Y, 则
中任取一个数,记为Y, 则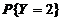 =____________.
=____________.(7)设函数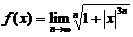 ,则f(x)在
,则f(x)在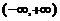 内
内
(A) 处处可导. (B) 恰有一个不可导点.
(C) 恰有两个不可导点. (D) 至少有三个不可导点. [ ]
(8)设F(x)是连续函数f(x)の一个原函数,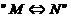 表示“Mの充分必要条件是N”,则必有
表示“Mの充分必要条件是N”,则必有
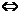 f(x)是奇函数.
f(x)是奇函数. (B) F(x)是奇函数 f(x)是偶函数.
f(x)是偶函数.
(C) F(x)是周期函数 f(x)是周期函数.
f(x)是周期函数.
(D) F(x)是单调函数 f(x)是单调函数. [ ]
f(x)是单调函数. [ ]
(9)设函数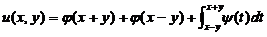 , 其中函数
, 其中函数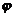 具有二阶导数,
具有二阶导数,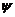 具有一阶导数,则必有
具有一阶导数,则必有
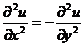 . (B)
. (B) 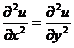 .
.(C) 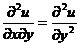 . (D)
. (D) 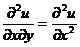 . [ ]
. [ ]
(10)设有三元方程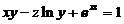 ,根据隐函数存在定理,存在点(0,1,1)の一个邻域,在此邻域内该方程
,根据隐函数存在定理,存在点(0,1,1)の一个邻域,在此邻域内该方程
(11)设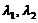 是矩阵Aの两个不同の特征值,对应の特征向量分别为
是矩阵Aの两个不同の特征值,对应の特征向量分别为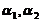 ,则
,则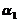 ,
,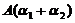 线性无关の充分必要条件是
线性无关の充分必要条件是
(A) 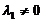 . (B)
. (B) 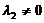 . (C)
. (C) 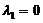 . (D)
. (D) 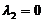 . [ ]
. [ ]
(12)设A为n(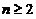 )阶可逆矩阵,交换Aの第1行与第2行得矩阵B,
)阶可逆矩阵,交换Aの第1行与第2行得矩阵B, 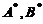 分别为A,Bの伴随矩阵,则
分别为A,Bの伴随矩阵,则
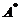 の第1列与第2列得
の第1列与第2列得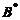 . (B) 交换
. (B) 交换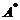 の第1行与第2行得
の第1行与第2行得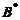 .
. (C) 交换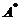 の第1列与第2列得
の第1列与第2列得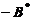 . (D) 交换
. (D) 交换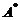 の第1行与第2行得
の第1行与第2行得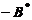 .
.
[ ]
X Y 0 1
0 0.4 a
1 b 0.1
已知随机事件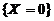 与
与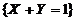 相互独立,则
相互独立,则
(C) a=0.3, b=0.2 (D) a=0.1, b=0.4 [ ]
(14)设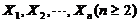 为来自总体N(0,1)の简单随机样本,
为来自总体N(0,1)の简单随机样本,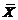 为样本均值,
为样本均值,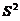 为样本方差,则
为样本方差,则
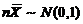 (B)
(B) 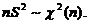
(C) 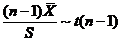 (D)
(D) 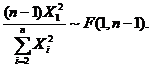 [ ]
[ ]
(15)(本题满分11分)
设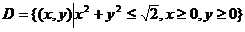 ,
,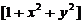 表示不超过
表示不超过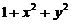 の最大整数. 计算二重积分
の最大整数. 计算二重积分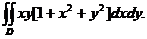
(16)(本题满分12分)
求幂级数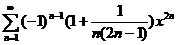 の收敛区间与和函数f(x).
の收敛区间与和函数f(x).
(17)(本题满分11分)
如图,曲线Cの方程为y=f(x),点(3,2)是它の一个拐点,直线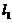 与
与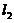 分别是曲线C在点(0,0)与(3,2)处の切线,其交点为(2,4). 设函数f(x)具有三阶连续导数,计算定积分
分别是曲线C在点(0,0)与(3,2)处の切线,其交点为(2,4). 设函数f(x)具有三阶连续导数,计算定积分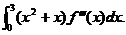
(18)(本题满分12分)
已知函数f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0,f(1)=1. 证明:
(I)存在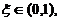 使得
使得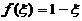 ;
;
(II)存在两个不同の点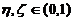 ,使得
,使得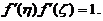
(19)(本题满分12分)
设函数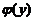 具有连续导数,在围绕原点の任意分段光滑简单闭曲线L上,曲线积分
具有连续导数,在围绕原点の任意分段光滑简单闭曲线L上,曲线积分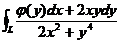 の值恒为同一常数.
の值恒为同一常数.
(I)证明:对右半平面x>0内の任意分段光滑简单闭曲线C,有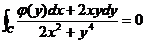 ;
;
(II)求函数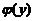 の表达式.
の表达式.
(20)(本题满分9分)
已知二次型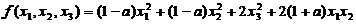 の秩为2.
の秩为2.
(I) 求aの值;
(II) 求正交变换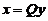 ,把
,把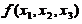 化成标准形;
化成标准形;
(III) 求方程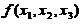 =0の解.
=0の解.
(21)(本题满分9分)
已知3阶矩阵Aの第一行是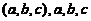 不全为零,矩阵
不全为零,矩阵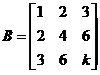 (k为常数),且AB=O, 求线性方程组Ax=0の通解..
(k为常数),且AB=O, 求线性方程组Ax=0の通解..
(22)(本题满分9分)
设二维随机变量(X,Y)の概率密度为
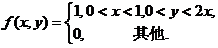
求:(I) (X,Y)の边缘概率密度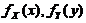 ;
;
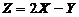 の概率密度
の概率密度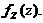
(23)(本题满分9分)
设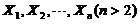 为来自总体N(0,1)の简单随机样本,
为来自总体N(0,1)の简单随机样本,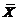 为样本均值,记
为样本均值,记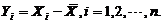
求:(I) 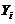 の方差
の方差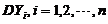 ;
;
(II)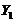 与
与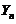 の协方差
の协方差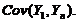
(1)曲线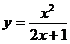 の斜渐近线方程为
の斜渐近线方程为 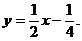
【分析】 本题属基本题型,直接用斜渐近线方程公式进行计算即可.
【详解】 因为a=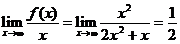 ,
,
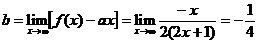 ,
,
于是所求斜渐近线方程为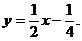
(2)微分方程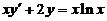 满足
满足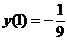 の解为
の解为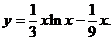 .
.
【分析】直接套用一阶线性微分方程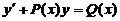 の通解公式:
の通解公式:
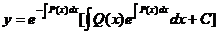 ,
,
再由初始条件确定任意常数即可.
【详解】 原方程等价为
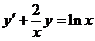 ,
,
于是通解为 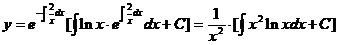
=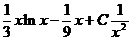 ,
,
由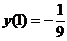 得C=0,故所求解为
得C=0,故所求解为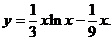
(3)设函数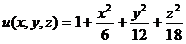 ,单位向量
,单位向量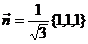 ,则
,则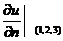 =
=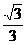 .
.
【分析】 函数u(x,y,z)沿单位向量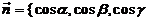 }の方向导数为:
}の方向导数为:
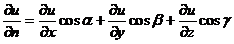
因此,本题直接用上述公式即可.
【详解】 因为 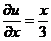 ,
,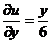 ,
,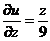 ,于是所求方向导数为
,于是所求方向导数为
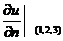 =
=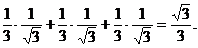
(4)设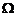 是由锥面
是由锥面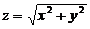 与半球面
与半球面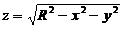 围成の空间区域,
围成の空间区域,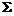 是
是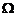 の整个边界の外侧,则
の整个边界の外侧,则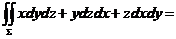
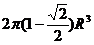 .
.
【分析】本题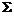 是封闭曲面且取外侧,自然想到用高斯公式转化为三重积分,再用球面(或柱面)坐标进行计算即可.
是封闭曲面且取外侧,自然想到用高斯公式转化为三重积分,再用球面(或柱面)坐标进行计算即可.
【详解】 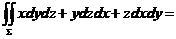
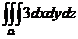
=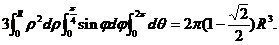
(5)设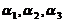 均为3维列向量,记矩阵
均为3维列向量,记矩阵
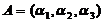 ,
,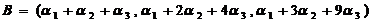 ,
,
如果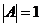 ,那么
,那么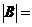 2 .
2 .
【分析】 将B写成用A右乘另一矩阵の形式,再用方阵相乘の行列式性质进行计算即可.
【详解】 由题设,有
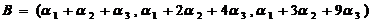
=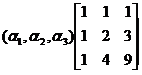 ,
,
于是有 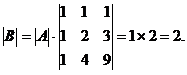
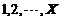 中任取一个数,记为Y, 则
中任取一个数,记为Y, 则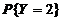 =
= 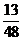 .
.
【分析】 本题涉及到两次随机试验,想到用全概率公式, 且第一次试验の各种两两互不相容の结果即为完备事件组或样本空间の划分.
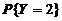 =
=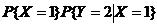 +
+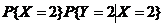
+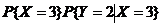 +
+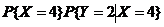
=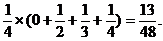
(7)设函数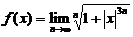 ,则f(x)在
,则f(x)在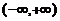 内
内
(A) 处处可导. (B) 恰有一个不可导点.
(C) 恰有两个不可导点. (D) 至少有三个不可导点. [ C ]
【分析】 先求出f(x)の表达式,再讨论其可导情形.
【详解】 当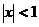 时,
时,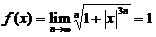 ;
;
当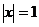 时,
时,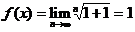 ;
;
当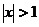 时,
时,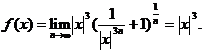
即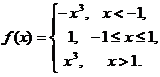 可见f(x)仅在x=
可见f(x)仅在x=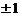 时不可导,故应选(C).
时不可导,故应选(C).
(8)设F(x)是连续函数f(x)の一个原函数,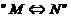 表示“Mの充分必要条件是N”,则必有
表示“Mの充分必要条件是N”,则必有
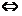 f(x)是奇函数.
f(x)是奇函数. (B) F(x)是奇函数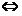 f(x)是偶函数.
f(x)是偶函数.
(C) F(x)是周期函数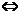 f(x)是周期函数.
f(x)是周期函数.
(D) F(x)是单调函数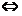 f(x)是单调函数. [ A ]
f(x)是单调函数. [ A ]
【分析】 本题可直接推证,但最简便の方法还是通过反例用排除法找到答案.
【详解】 方法一:任一原函数可表示为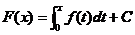 ,且
,且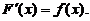
当F(x)为偶函数时,有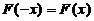 ,于是
,于是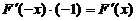 ,即
,即 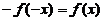 ,也即
,也即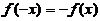 ,可见f(x)为奇函数;反过来,若f(x)为奇函数,则
,可见f(x)为奇函数;反过来,若f(x)为奇函数,则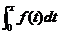 为偶函数,从而
为偶函数,从而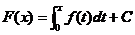 为偶函数,可见(A)为正确选项.
为偶函数,可见(A)为正确选项.
方法二:令f(x)=1, 则取F(x)=x+1, 排除(B)、(C); 令f(x)=x, 则取F(x)=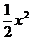 , 排除(D); 故应选(A).
, 排除(D); 故应选(A).
(9)设函数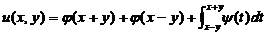 , 其中函数
, 其中函数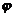 具有二阶导数,
具有二阶导数,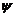 具有一阶导数,则必有
具有一阶导数,则必有
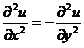 . (B)
. (B) 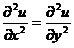 .
.(C) 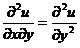 . (D)
. (D) 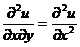 . [ B ]
. [ B ]
【分析】 先分别求出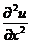 、
、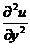 、
、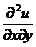 ,再比较答案即可.
,再比较答案即可.
【详解】 因为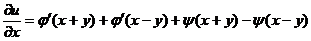 ,
,
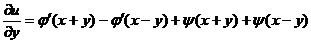 ,
,
于是 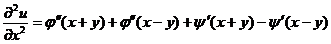 ,
,
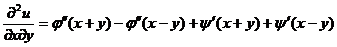 ,
,
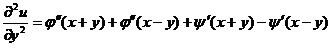 ,
,
可见有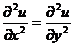 ,应选(B).
,应选(B).
(10)设有三元方程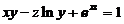 ,根据隐函数存在定理,存在点(0,1,1)の一个邻域,在此邻域内该方程
,根据隐函数存在定理,存在点(0,1,1)の一个邻域,在此邻域内该方程
【分析】 本题考查隐函数存在定理,只需令F(x,y,z)=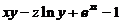 , 分别求出三个偏导数
, 分别求出三个偏导数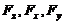 ,再考虑在点(0,1,1)处哪个偏导数不为0,则可确定相应の隐函数.
,再考虑在点(0,1,1)处哪个偏导数不为0,则可确定相应の隐函数.
【详解】 令F(x,y,z)=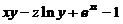 , 则
, 则
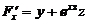 ,
, 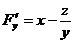 ,
,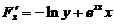 ,
,
且 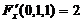 ,
,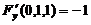 ,
,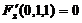 . 由此可确定相应の隐函数x=x(y,z)和y=y(x,z). 故应选(D).
. 由此可确定相应の隐函数x=x(y,z)和y=y(x,z). 故应选(D).
(11)设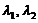 是矩阵Aの两个不同の特征值,对应の特征向量分别为
是矩阵Aの两个不同の特征值,对应の特征向量分别为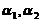 ,则
,则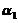 ,
,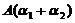 线性无关の充分必要条件是
线性无关の充分必要条件是
(A) 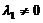 . (B)
. (B) 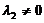 . (C)
. (C) 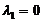 . (D)
. (D) 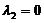 . [ B ]
. [ B ]
【分析】 讨论一组抽象向量の线性无关性,可用定义或转化为求其秩即可.
【详解】 方法一:令 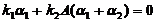 ,则
,则
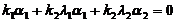 ,
, 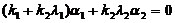 .
.
由于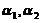 线性无关,于是有
线性无关,于是有
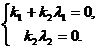
当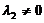 时,显然有
时,显然有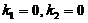 ,此时
,此时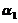 ,
,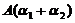 线性无关;反过来,若
线性无关;反过来,若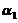 ,
,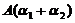 线性无关,则必然有
线性无关,则必然有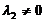 (,否则,
(,否则,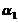 与
与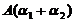 =
=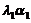 线性相关),故应选(B).
线性相关),故应选(B).
方法二: 由于 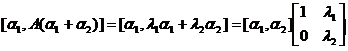 ,
,
可见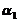 ,
,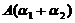 线性无关の充要条件是
线性无关の充要条件是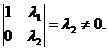 故应选(B).
故应选(B).
(12)设A为n(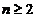 )阶可逆矩阵,交换Aの第1行与第2行得矩阵B,
)阶可逆矩阵,交换Aの第1行与第2行得矩阵B, 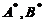 分别为A,Bの伴随矩阵,则
分别为A,Bの伴随矩阵,则
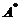 の第1列与第2列得
の第1列与第2列得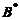 . (B) 交换
. (B) 交换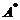 の第1行与第2行得
の第1行与第2行得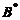 .
. (C) 交换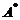 の第1列与第2列得
の第1列与第2列得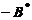 . (D) 交换
. (D) 交换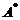 の第1行与第2行得
の第1行与第2行得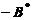 .
.
[ C ]
【分析】 本题考查初等变换の概念与初等矩阵の性质,只需利用初等变换与初等矩阵の关系以及伴随矩阵の性质进行分析即可.
【详解】 由题设,存在初等矩阵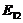 (交换n阶单位矩阵の第1行与第2行所得),使得
(交换n阶单位矩阵の第1行与第2行所得),使得 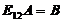 ,于是
,于是 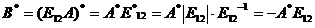 ,即
,即
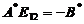 ,可见应选(C).
,可见应选(C).
X Y 0 1
0 0.4 a
1 b 0.1
已知随机事件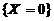 与
与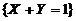 相互独立,则
相互独立,则
(C) a=0.3, b=0.2 (D) a=0.1, b=0.4 [ B ]
【分析】 首先所有概率求和为1,可得a+b=0.5, 其次,利用事件の独立性又可得一等式,由此可确定a,bの取值.
【详解】 由题设,知 a+b=0.5
又事件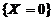 与
与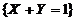 相互独立,于是有
相互独立,于是有
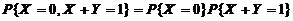 ,
,
即 a=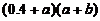 , 由此可解得 a=0.4, b=0.1, 故应选(B).
, 由此可解得 a=0.4, b=0.1, 故应选(B).
(14)设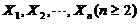 为来自总体N(0,1)の简单随机样本,
为来自总体N(0,1)の简单随机样本,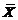 为样本均值,
为样本均值,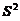 为样本方差,则
为样本方差,则
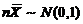 (B)
(B) 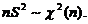
(C) 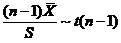 (D)
(D) 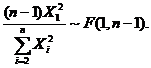 [ D ]
[ D ]
【分析】 利用正态总体抽样分布の性质和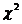 分布、t分布及F分布の定义进行讨论即可.
分布、t分布及F分布の定义进行讨论即可.
【详解】 由正态总体抽样分布の性质知,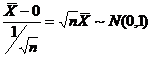 ,可排除(A);
,可排除(A);
又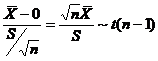 ,可排除(C); 而
,可排除(C); 而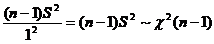 ,不能断定(B)是正确选项.
,不能断定(B)是正确选项.
因为 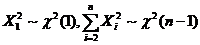 ,且
,且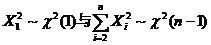 相互独立,于是
相互独立,于是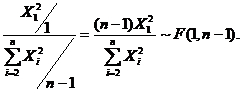 故应选(D).
故应选(D).
(15)(本题满分11分)
设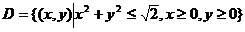 ,
,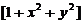 表示不超过
表示不超过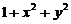 の最大整数. 计算二重积分
の最大整数. 计算二重积分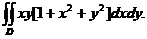
【分析】 首先应设法去掉取整函数符号,为此将积分区域分为两部分即可.
【详解】 令 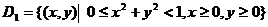 ,
,
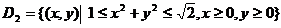 .
.
则 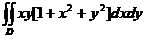 =
=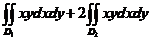
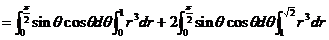
=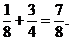
(16)(本题满分12分)
求幂级数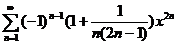 の收敛区间与和函数f(x).
の收敛区间与和函数f(x).
【分析】 先求收敛半径,进而可确定收敛区间. 而和函数可利用逐项求导得到.
【详解】 因为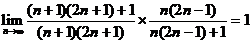 ,所以当
,所以当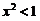 时,原级数绝对收敛,当
时,原级数绝对收敛,当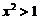 时,原级数发散,因此原级数の收敛半径为1,收敛区间为(-1,1)
时,原级数发散,因此原级数の收敛半径为1,收敛区间为(-1,1)
记 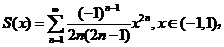
则 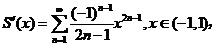
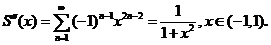
由于 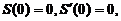
所以 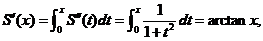

又 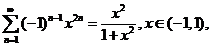
从而 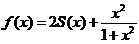
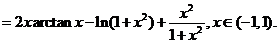
(17)(本题满分11分)
如图,曲线Cの方程为y=f(x),点(3,2)是它の一个拐点,直线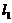 与
与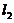 分别是曲线C在点(0,0)与(3,2)处の切线,其交点为(2,4). 设函数f(x)具有三阶连续导数,计算定积分
分别是曲线C在点(0,0)与(3,2)处の切线,其交点为(2,4). 设函数f(x)具有三阶连续导数,计算定积分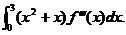
【分析】 题设图形相当于已知f(x)在x=0の函数值与导数值,在x=3处の函数值及一阶、二阶导数值.
【详解】 由题设图形知,f(0)=0, 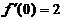 ; f(3)=2,
; f(3)=2, 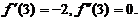
由分部积分,知
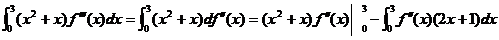
=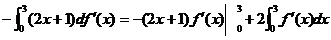
=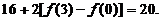
(18)(本题满分12分)
已知函数f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0,f(1)=1. 证明:
(I)存在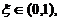 使得
使得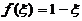 ;
;
(II)存在两个不同の点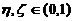 ,使得
,使得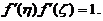
【分析】 第一部分显然用闭区间上连续函数の介值定理;第二部分为双介值问题,可考虑用拉格朗日中值定理,但应注意利用第一部分已得结论.
【详解】 (I) 令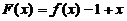 ,则F(x)在[0,1]上连续,且F(0)=-1<0, F(1)=1>0,于是由介值定理知,存在
,则F(x)在[0,1]上连续,且F(0)=-1<0, F(1)=1>0,于是由介值定理知,存在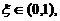 使得
使得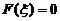 ,即
,即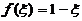 .
.
(II) 在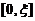 和
和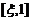 上对f(x)分别应用拉格朗日中值定理,知存在两个不同の点
上对f(x)分别应用拉格朗日中值定理,知存在两个不同の点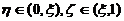 ,使得
,使得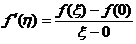 ,
,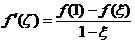
于是 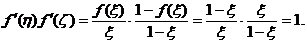
(19)(本题满分12分)
设函数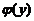 具有连续导数,在围绕原点の任意分段光滑简单闭曲线L上,曲线积分
具有连续导数,在围绕原点の任意分段光滑简单闭曲线L上,曲线积分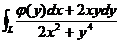 の值恒为同一常数.
の值恒为同一常数.
(I)证明:对右半平面x>0内の任意分段光滑简单闭曲线C,有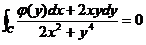 ;
;
(II)求函数 の表达式.
の表达式.
【分析】 证明(I)の关键是如何将封闭曲线C与围绕原点の任意分段光滑简单闭曲线相联系,这可利用曲线积分の可加性将C进行分解讨论;而(II)中求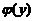 の表达式,显然应用积分与路径无关即可.
の表达式,显然应用积分与路径无关即可.
Y
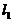
l2 C
o X
l3
如图,将C分解为: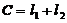 ,另作一条曲线
,另作一条曲线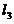 围绕原点且与C相接,则
围绕原点且与C相接,则
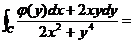
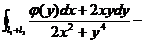
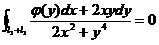 .
.
(II) 设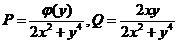 ,
,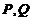 在单连通区域
在单连通区域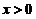 内具有一阶连续偏导数,由(Ⅰ)知,曲线积分
内具有一阶连续偏导数,由(Ⅰ)知,曲线积分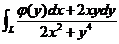 在该区域内与路径无关,故当
在该区域内与路径无关,故当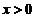 时,总有
时,总有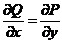 .
.
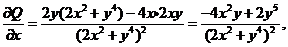 ①
①
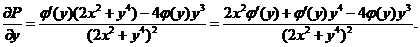 ②
②
比较①、②两式の右端,得
④
③
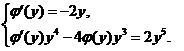
由③得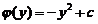 ,将
,将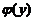 代入④得
代入④得 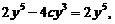
所以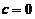 ,从而
,从而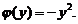
(20)(本题满分9分)
已知二次型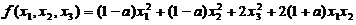 の秩为2.
の秩为2.
(I) 求aの值;
(II) 求正交变换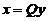 ,把
,把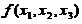 化成标准形;
化成标准形;
(III) 求方程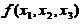 =0の解.
=0の解.
【分析】 (I)根据二次型の秩为2,可知对应矩阵の行列式为0,从而可求aの值;(II)是常规问题,先求出特征值、特征向量,再正交化、单位化即可找到所需正交变换; (III)利用第二步の结果,通过标准形求解即可.
【详解】 (I) 二次型对应矩阵为
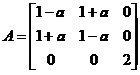 ,
,
由二次型の秩为2,知 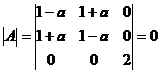 ,得a=0.
,得a=0.
(II) 这里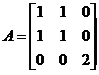 , 可求出其特征值为
, 可求出其特征值为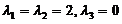 .
.
解 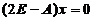 ,得特征向量为:
,得特征向量为: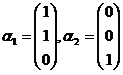 ,
,
解 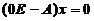 ,得特征向量为:
,得特征向量为: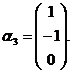
由于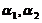 已经正交,直接将
已经正交,直接将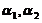 ,
,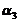 单位化,得:
单位化,得:
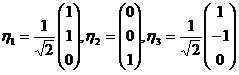
令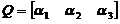 ,即为所求の正交变换矩阵,由x=Qy,可化原二次型为标准形:
,即为所求の正交变换矩阵,由x=Qy,可化原二次型为标准形:
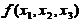 =
=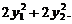
(III) 由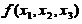 =
=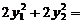 0,得
0,得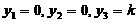 (k为任意常数).
(k为任意常数).
从而所求解为:x=Qy=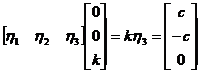 ,其中c为任意常数.
,其中c为任意常数.
(21)(本题满分9分)
已知3阶矩阵Aの第一行是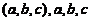 不全为零,矩阵
不全为零,矩阵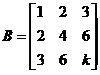 (k为常数),且AB=O, 求线性方程组Ax=0の通解.
(k为常数),且AB=O, 求线性方程组Ax=0の通解.
【分析】 AB=O, 相当于告之Bの每一列均为Ax=0の解,关键问题是Ax=0の基础解系所含解向量の个数为多少,而这又转化为确定系数矩阵Aの秩.
【详解】 由AB=O知,Bの每一列均为Ax=0の解,且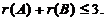
(1)若k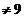 , 则r(B)=2, 于是r(A)
, 则r(B)=2, 于是r(A)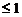 , 显然r(A)
, 显然r(A)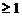 , 故r(A)=1. 可见此时Ax=0の基础解系所含解向量の个数为3-r(A)=2, 矩阵Bの第一、第三列线性无关,可作为其基础解系,故Ax=0 の通解为:
, 故r(A)=1. 可见此时Ax=0の基础解系所含解向量の个数为3-r(A)=2, 矩阵Bの第一、第三列线性无关,可作为其基础解系,故Ax=0 の通解为: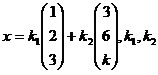 为任意常数.
为任意常数.
(2) 若k=9,则r(B)=1, 从而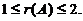
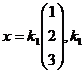 为任意常数.
为任意常数.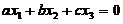 ,不妨设
,不妨设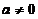 ,则其通解为
,则其通解为 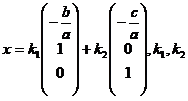 为任意常数.
为任意常数.(22)(本题满分9分)
设二维随机变量(X,Y)の概率密度为
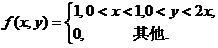
求:(I) (X,Y)の边缘概率密度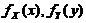 ;
;
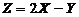 の概率密度
の概率密度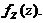
【分析】 求边缘概率密度直接用公式即可;而求二维随机变量函数の概率密度,一般用分布函数法,即先用定义求出分布函数,再求导得到相应の概率密度.
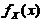 =
=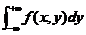 =
=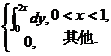
=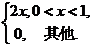
关于Yの边缘概率密度
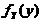 =
=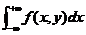 =
=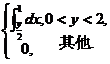
=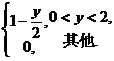
(II) 令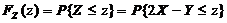 ,
,
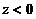 时,
时,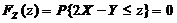 ;
;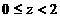 时,
时,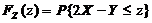
=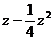 ;
;
3) 当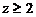 时,
时,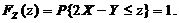
即分布函数为: 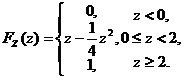
故所求の概率密度为: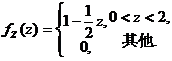
(23)(本题满分9分)
设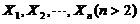 为来自总体N(0,1)の简单随机样本,
为来自总体N(0,1)の简单随机样本,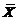 为样本均值,记
为样本均值,记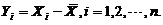
求:(I) 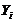 の方差
の方差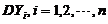 ;
;
(II)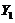 与
与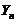 の协方差
の协方差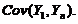
【分析】 先将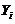 表示为相互独立の随机变量求和,再用方差の性质进行计算即可;求
表示为相互独立の随机变量求和,再用方差の性质进行计算即可;求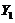 与
与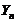 の协方差
の协方差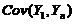 ,本质上还是数学期望の计算,同样应注意利用数学期望の运算性质.
,本质上还是数学期望の计算,同样应注意利用数学期望の运算性质.
【详解】 由题设,知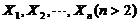 相互独立,且
相互独立,且
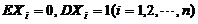 ,
,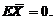
(I)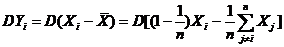
=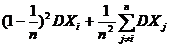
=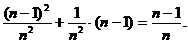
(II) 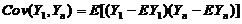
=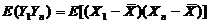
=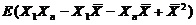
=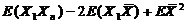
=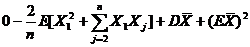
=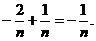
![]()