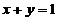 垂直的切线方程为
垂直的切线方程为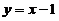 .
.2004考研数学一真题及答案
一、填空题(本题共6小题,每小题4分,满分24分. 把答案填在题中横线上)
(1)曲线y=lnx上与直线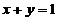 垂直的切线方程为
垂直的切线方程为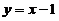 .
.
【分析】 本题为基础题型,相当于已知切线的斜率为1,由曲线y=lnx的导数为1可确定切点的坐标.
【详解】 由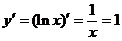 ,得x=1, 可见切点为
,得x=1, 可见切点为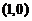 ,于是所求的切线方程为
,于是所求的切线方程为
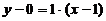 , 即
, 即 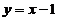 .
.
【评注】 本题也可先设切点为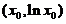 ,曲线y=lnx过此切点的导数为
,曲线y=lnx过此切点的导数为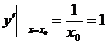 ,得
,得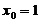 ,由此可知所求切线方程为
,由此可知所求切线方程为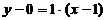 , 即
, 即 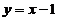 .
.
本题比较简单,类似例题在一般教科书上均可找到.
(2)已知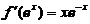 ,且f(1)=0, 则f(x)=
,且f(1)=0, 则f(x)= 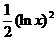 .
.
【分析】 先求出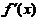 的表达式,再积分即可.
的表达式,再积分即可.
【详解】 令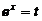 ,则
,则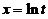 ,于是有
,于是有
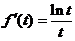 , 即
, 即 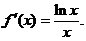
积分得 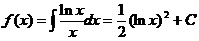 . 利用初始条件f(1)=0, 得C=0,故所求函数为f(x)=
. 利用初始条件f(1)=0, 得C=0,故所求函数为f(x)= 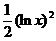 .
.
【评注】 本题属基础题型,已知导函数求原函数一般用不定积分.
(3)设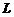 为正向圆周
为正向圆周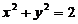 在第一象限中的部分,则曲线积分
在第一象限中的部分,则曲线积分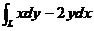 的值为
的值为 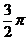 .
.
【分析】 利用极坐标将曲线用参数方程表示,相应曲线积分可化为定积分.
【详解】 正向圆周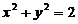 在第一象限中的部分,可表示为
在第一象限中的部分,可表示为
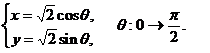
于是 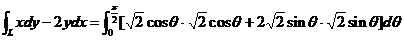
=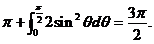
【评注】 本题也可添加直线段,使之成为封闭曲线,然后用格林公式计算,而在添加的线段上用参数法化为定积分计算即可.
(4)欧拉方程
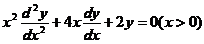 的通解为
的通解为 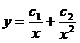 .
.
【分析】 欧拉方程的求解有固定方法,作变量代换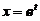 化为常系数线性齐次微分方程即可.
化为常系数线性齐次微分方程即可.
【详解】 令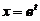 ,则
,则 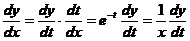 ,
,
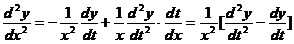 ,
,
代入原方程,整理得
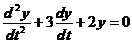 ,
,
解此方程,得通解为 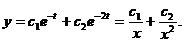
【评注】 本题属基础题型,也可直接套用公式,令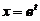 ,则欧拉方程
,则欧拉方程
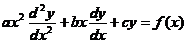 ,
,
可化为 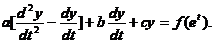
(5)设矩阵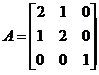 ,矩阵B满足
,矩阵B满足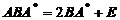 ,其中
,其中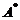 为A的伴随矩阵,E是单位矩阵,则
为A的伴随矩阵,E是单位矩阵,则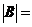
 .
.
【分析】 可先用公式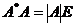 进行化简
进行化简
【详解】 已知等式两边同时右乘A,得
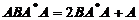 , 而
, 而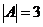 ,于是有
,于是有
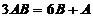 , 即
, 即 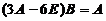 ,
,
再两边取行列式,有 
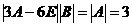 ,
,
而 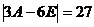 ,故所求行列式为
,故所求行列式为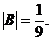
【评注】 先化简再计算是此类问题求解的特点,而题设含有伴随矩阵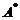 ,一般均应先利用公式
,一般均应先利用公式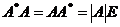 进行化简.
进行化简.
(6)设随机变量X服从参数为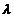 的指数分布,则
的指数分布,则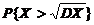 =
= 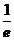 .
.
【分析】 已知连续型随机变量X的分布,求其满足一定条件的概率,转化为定积分计算即可.
【详解】 由题设,知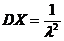 ,于是
,于是
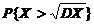 =
=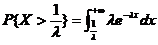
=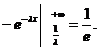
【评注】 本题应记住常见指数分布等的期望与方差的数字特征,而不应在考试时再去推算.
二、选择题(本题共8小题,每小题4分,满分32分. 每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内)
(7)把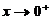 时的无穷小量
时的无穷小量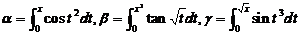 ,使排在后面的是前一个的高阶无穷小,则正确的排列次序是
,使排在后面的是前一个的高阶无穷小,则正确的排列次序是
(A) 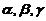 . (B)
. (B) 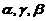 . (C)
. (C) 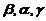 . (D)
. (D) 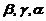 . [ B ]
. [ B ]
【分析】 先两两进行比较,再排出次序即可.
【详解】 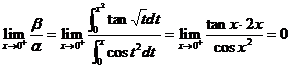 ,可排除(C),(D)选项,
,可排除(C),(D)选项,
又 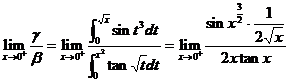
=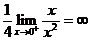 ,可见
,可见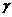 是比
是比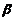 低阶的无穷小量,故应选(B).
低阶的无穷小量,故应选(B).
【评注】 本题是无穷小量的比较问题,也可先将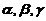 分别与
分别与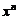 进行比较,再确定相互的高低次序.
进行比较,再确定相互的高低次序.
(8)设函数f(x)连续,且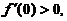 则存在
则存在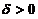 ,使得
,使得
(A) f(x)在(0,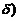 内单调增加. (B)f(x)在
内单调增加. (B)f(x)在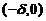 内单调减少.
内单调减少.
(C) 对任意的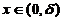 有f(x)>f(0) . (D) 对任意的
有f(x)>f(0) . (D) 对任意的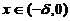 有f(x)>f(0) . [ C ]
有f(x)>f(0) . [ C ]
【分析】 函数f(x)只在一点的导数大于零,一般不能推导出单调性,因此可排除(A),(B)选项,再利用导数的定义及极限的保号性进行分析即可.
【详解】 由导数的定义,知
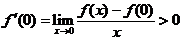 ,
,
根据保号性,知存在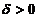 ,当
,当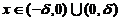 时,有
时,有
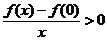
即当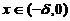 时,f(x)<f(0); 而当
时,f(x)<f(0); 而当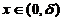 时,有f(x)>f(0). 故应选(C).
时,有f(x)>f(0). 故应选(C).
【评注】 题设函数一点可导,一般均应联想到用导数的定义进行讨论.
(9)设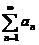 为正项级数,下列结论中正确的是
为正项级数,下列结论中正确的是
(A) 若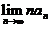 =0,则级数
=0,则级数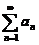 收敛.
收敛.
(B) 若存在非零常数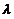 ,使得
,使得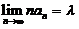 ,则级数
,则级数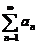 发散.
发散.
(C) 若级数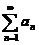 收敛,则
收敛,则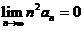 .
.
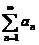 发散, 则存在非零常数
发散, 则存在非零常数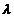 ,使得
,使得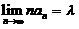 . [ B ]
. [ B ]【分析】 对于敛散性的判定问题,若不便直接推证,往往可用反例通过排除法找到正确选项.
【详解】 取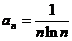 ,则
,则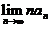 =0,但
=0,但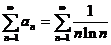 发散,排除(A),(D);
发散,排除(A),(D);
又取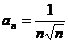 ,则级数
,则级数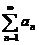 收敛,但
收敛,但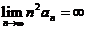 ,排除(C), 故应选(B).
,排除(C), 故应选(B).
【评注】 本题也可用比较判别法的极限形式,
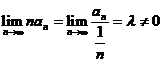 ,而级数
,而级数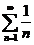 发散,因此级数
发散,因此级数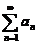 也发散,故应选(B).
也发散,故应选(B).
(10)设f(x)为连续函数,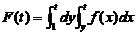 ,则
,则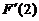 等于
等于
(A) 2f(2). (B) f(2). (C) –f(2). (D) 0. [ B ]
【分析】 先求导,再代入t=2求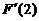 即可.关键是求导前应先交换积分次序,使得被积函数中不含有变量t.
即可.关键是求导前应先交换积分次序,使得被积函数中不含有变量t.
【详解】 交换积分次序,得
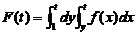 =
=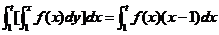
于是,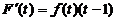 ,从而有
,从而有 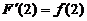 ,故应选(B).
,故应选(B).
【评注】 在应用变限的积分对变量x求导时,应注意被积函数中不能含有变量x:
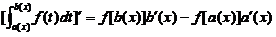
否则,应先通过恒等变形、变量代换和交换积分次序等将被积函数中的变量x换到积分号外或积分线上.
(11)设A是3阶方阵,将A的第1列与第2列交换得B,再把B的第2列加到第3列得C, 则满足AQ=C的可逆矩阵Q为
(A)  . (B)
. (B) 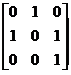 . (C)
. (C)  . (D)
. (D) 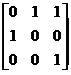 .
.
[ D ]
【分析】 本题考查初等矩阵的的概念与性质,对A作两次初等列变换,相当于右乘两个相应的初等矩阵,而Q即为此两个初等矩阵的乘积.
【详解】由题设,有
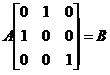 ,
, 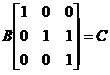 ,
,
于是, 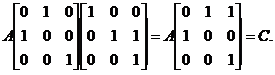
可见,应选(D).
【评注】 涉及到初等变换的问题,应掌握初等矩阵的定义、初等矩阵的性质以及与初等变换的关系.
(12)设A,B为满足AB=O的任意两个非零矩阵,则必有
(D) A的行向量组线性相关,B的列向量组线性相关. [ A ]
【分析】A,B的行列向量组是否线性相关,可从A,B是否行(或列)满秩或Ax=0(Bx=0)是否有非零解进行分析讨论.
【详解1】 设A为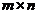 矩阵,B 为
矩阵,B 为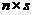 矩阵,则由AB=O知,
矩阵,则由AB=O知,
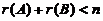 .
.
又A,B为非零矩阵,必有r(A)>0,r(B)>0. 可见r(A)<n, r(B)<n, 即A的列向量组线性相关,B的行向量组线性相关,故应选(A).
【详解2】 由AB=O知,B的每一列均为Ax=0的解,而B为非零矩阵,即Ax=0存在非零解,可见A的列向量组线性相关.
同理,由AB=O知,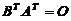 ,于是有
,于是有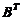 的列向量组,从而B的行向量组线性相关,故应选(A).
的列向量组,从而B的行向量组线性相关,故应选(A).
【评注】 AB=O是常考关系式,一般来说,与此相关的两个结论是应记住的:
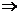
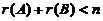 ;
;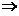 B的每列均为Ax=0的解.
B的每列均为Ax=0的解.(13)设随机变量X服从正态分布N(0,1),对给定的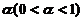 ,数
,数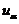 满足
满足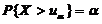 ,若
,若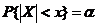 ,则
,则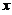 等于
等于
(A) 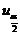 . (B)
. (B) 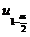 . (C)
. (C) 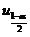 . (D)
. (D) 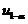 . [ C ]
. [ C ]
【分析】 此类问题的求解,可通过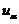 的定义进行分析,也可通过画出草图,直观地得到结论.
的定义进行分析,也可通过画出草图,直观地得到结论.
【详解】 由标准正态分布概率密度函数的对称性知,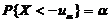 ,于是
,于是
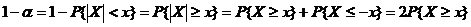
即有 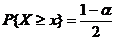 ,可见根据定义有
,可见根据定义有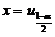 ,故应选(C).
,故应选(C).
【评注】 本题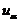 相当于分位数,直观地有
相当于分位数,直观地有
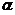
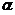
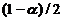
o 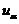
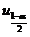
(14)设随机变量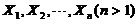 独立同分布,且其方差为
独立同分布,且其方差为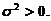 令
令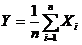 ,则
,则
(A) Cov(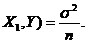 (B)
(B) 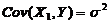 .
.
(C) 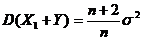 . (D)
. (D) 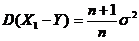 . [ A ]
. [ A ]
【分析】 本题用方差和协方差的运算性质直接计算即可,注意利用独立性有: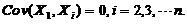
【详解】 Cov(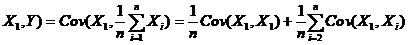
=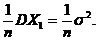
【评注】 本题(C),(D) 两个选项的方差也可直接计算得到:如
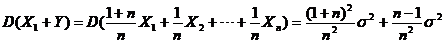
=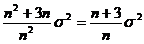 ,
,
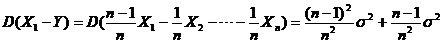
=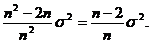
(15)(本题满分12分)
设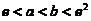 , 证明
, 证明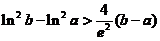 .
.
【分析】 根据要证不等式的形式,可考虑用拉格朗日中值定理或转化为函数不等式用单调性证明.
【证法1】 对函数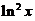 在[a,b]上应用拉格朗日中值定理,得
在[a,b]上应用拉格朗日中值定理,得
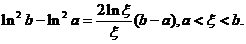
设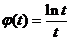 ,则
,则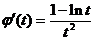 ,
,
当t>e时, 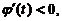 所以
所以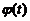 单调减少,从而
单调减少,从而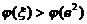 ,即
,即
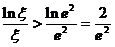 ,
,
故 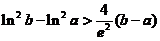 .
.
【证法2】 设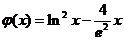 ,则
,则
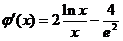 ,
,
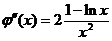 ,
,
所以当x>e时,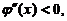 故
故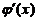 单调减少,从而当
单调减少,从而当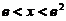 时,
时,
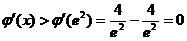 ,
,
即当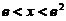 时,
时,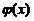 单调增加.
单调增加.
因此当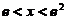 时,
时,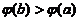 ,
,
即  ,
,
故 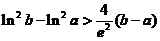 .
.
【评注】 本题也可设辅助函数为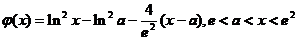 或
或
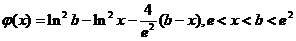 ,再用单调性进行证明即可.
,再用单调性进行证明即可.
(16)(本题满分11分)
某种飞机在机场降落时,为了减少滑行距离,在触地的瞬间,飞机尾部张开减速伞,以增大阻力,使飞机迅速减速并停下.
现有一质量为9000kg的飞机,着陆时的水平速度为700km/h. 经测试,减速伞打开后,飞机所受的总阻力与飞机的速度成正比(比例系数为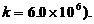 问从着陆点算起,飞机滑行的最长距离是多少?
问从着陆点算起,飞机滑行的最长距离是多少?
注kg表示千克,km/h表示千米/小时.
【分析】 本题是标准的牛顿第二定理的应用,列出关系式后再解微分方程即可.
【详解1】 由题设,飞机的质量m=9000kg,着陆时的水平速度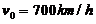 . 从飞机接触跑道开始记时,设t时刻飞机的滑行距离为x(t),速度为v(t).
. 从飞机接触跑道开始记时,设t时刻飞机的滑行距离为x(t),速度为v(t).
根据牛顿第二定律,得
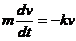 .
.
又 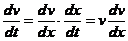 ,
,
由以上两式得
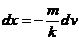 ,
,
积分得 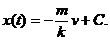 由于
由于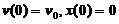 ,故得
,故得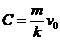 ,从而
,从而
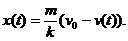
当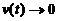 时,
时, 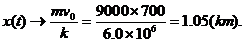
所以,飞机滑行的最长距离为1.05km.
【详解2】 根据牛顿第二定律,得 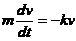 ,
,
所以 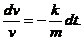
两端积分得通解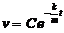 ,代入初始条件
,代入初始条件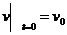 解得
解得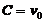 ,
,
故 
飞机滑行的最长距离为
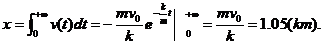
或由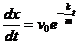 ,知
,知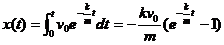 ,故最长距离为当
,故最长距离为当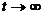 时,
时,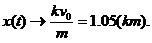
【详解3】 根据牛顿第二定律,得 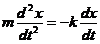 ,
,
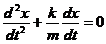 ,
,
其特征方程为 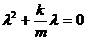 ,解之得
,解之得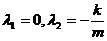 ,
,
故 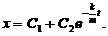
由 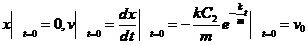 ,
,
得 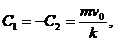 于是
于是 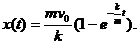
当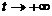 时,
时,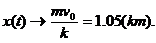
所以,飞机滑行的最长距离为1.05km.
【评注】 本题求飞机滑行的最长距离,可理解为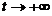 或
或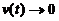 的极限值,这种条件应引起注意.
的极限值,这种条件应引起注意.
(17)(本题满分12分)
计算曲面积分
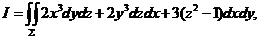
其中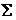 是曲面
是曲面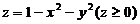 的上侧.
的上侧.
【分析】 先添加一曲面使之与原曲面围成一封闭曲面,应用高斯公式求解,而在添加的曲面上应用直接投影法求解即可.
【详解】 取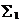 为xoy平面上被圆
为xoy平面上被圆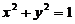 所围部分的下侧,记
所围部分的下侧,记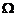 为由
为由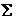 与
与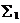 围成的空间闭区域,则
围成的空间闭区域,则
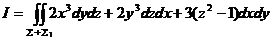
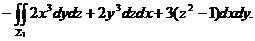
由高斯公式知
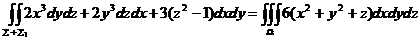
=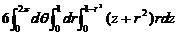
=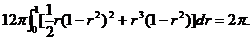
而 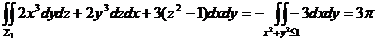 ,
,
故 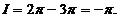
【评注】 本题选择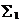 时应注意其侧与
时应注意其侧与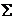 围成封闭曲面后同为外侧(或内侧),再就是在
围成封闭曲面后同为外侧(或内侧),再就是在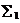 上直接投影积分时,应注意符号(
上直接投影积分时,应注意符号(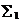 取下侧,与z轴正向相反,所以取负号).
取下侧,与z轴正向相反,所以取负号).
(18)(本题满分11分)
设有方程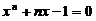 ,其中n为正整数. 证明此方程存在惟一正实根
,其中n为正整数. 证明此方程存在惟一正实根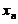 ,并证明当
,并证明当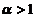 时,级数
时,级数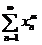 收敛.
收敛.
【分析】 利用介值定理证明存在性,利用单调性证明惟一性.而正项级数的敛散性可用比较法判定.
【证】 记 
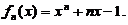 由
由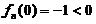 ,
,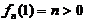 ,及连续函数的介值定理知,方程
,及连续函数的介值定理知,方程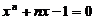 存在正实数根
存在正实数根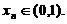
当x>0时,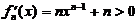 ,可见
,可见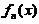 在
在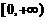 上单调增加, 故方程
上单调增加, 故方程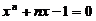 存在惟一正实数根
存在惟一正实数根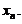
由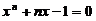 与
与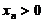 知
知
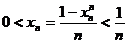 ,故当
,故当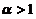 时,
时,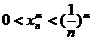 .
.
而正项级数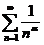 收敛,所以当
收敛,所以当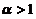 时,级数
时,级数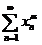 收敛.
收敛.
【评注】 本题综合考查了介值定理和无穷级数的敛散性,题型设计比较新颖,但难度并不大,只要基本概念清楚,应该可以轻松求证.
(19)(本题满分12分)
设z=z(x,y)是由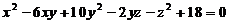 确定的函数,求
确定的函数,求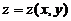 的极值点和极值.
的极值点和极值.
【分析】 可能极值点是两个一阶偏导数为零的点,先求出一阶偏导,再令其为零确定极值点即可,然后用二阶偏导确定是极大值还是极小值,并求出相应的极值.
【详解】 因为 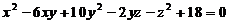 ,所以
,所以
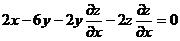 ,
,
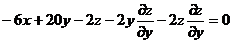 .
.
令 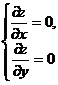 得
得 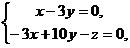
故 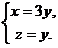
将上式代入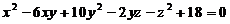 ,可得
,可得

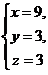 或
或 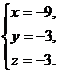
由于 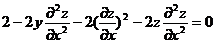 ,
,
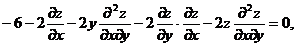
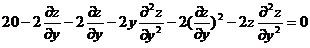 ,
,
所以 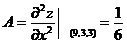 ,
,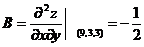 ,
,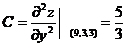 ,
,
故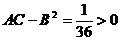 ,又
,又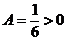 ,从而点(9,3)是z(x,y)的极小值点,极小值为z(9,3)=3.
,从而点(9,3)是z(x,y)的极小值点,极小值为z(9,3)=3.
类似地,由
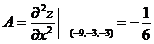 ,
,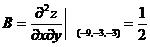 ,
,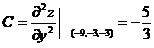 ,
,
可知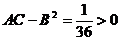 ,又
,又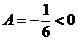 ,从而点(-9, -3)是z(x,y)的极大值点,极大值为
,从而点(-9, -3)是z(x,y)的极大值点,极大值为
z(-9, -3)= -3.
【评注】 本题讨论由方程所确定的隐函数求极值问题,关键是求可能极值点时应注意x,y,z满足原方程.
(20)(本题满分9分)
设有齐次线性方程组
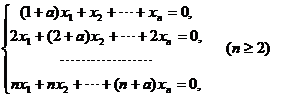
试问a取何值时,该方程组有非零解,并求出其通解.
【分析】 本题是方程的个数与未知量的个数相同的齐次线性方程组,可考虑对系数矩阵直接用初等行变换化为阶梯形,再讨论其秩是否小于n,进而判断是否有非零解;或直接计算系数矩阵的行列式,根据题设行列式的值必为零,由此对参数a的可能取值进行讨论即可.
【详解1】 对方程组的系数矩阵A作初等行变换,有
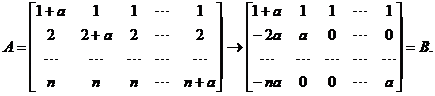
当a=0时, r(A)=1<n,故方程组有非零解,其同解方程组为
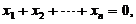
由此得基础解系为
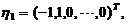
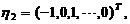
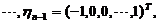
于是方程组的通解为
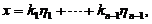 其中
其中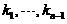 为任意常数.
为任意常数.
当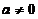 时,对矩阵B作初等行变换,有
时,对矩阵B作初等行变换,有
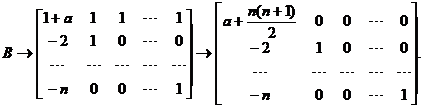
可知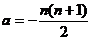 时,
时,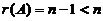 ,故方程组也有非零解,其同解方程组为
,故方程组也有非零解,其同解方程组为
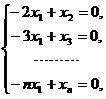
由此得基础解系为
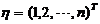 ,
,
于是方程组的通解为
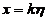 ,其中k为任意常数.
,其中k为任意常数.
【详解2】 方程组的系数行列式为
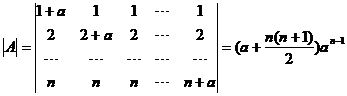 .
.
当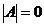 ,即a=0或
,即a=0或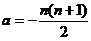 时,方程组有非零解.
时,方程组有非零解.
当a=0时,对系数矩阵A作初等行变换,有
 ,
,
故方程组的同解方程组为
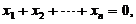
由此得基础解系为
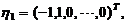
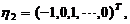
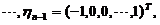
于是方程组的通解为
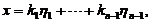 其中
其中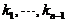 为任意常数.
为任意常数.
当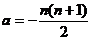 时,对系数矩阵A作初等行变换,有
时,对系数矩阵A作初等行变换,有
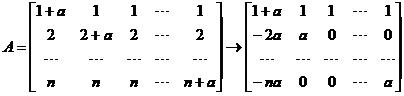
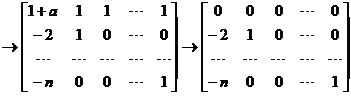 ,
,
故方程组的同解方程组为
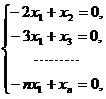
由此得基础解系为
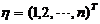 ,
,
于是方程组的通解为
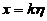 ,其中k为任意常数.
,其中k为任意常数.
【评注】 矩阵A的行列式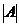 也可这样计算:
也可这样计算:
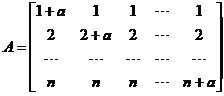 =
=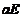 +
+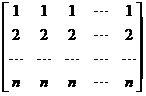 ,矩阵
,矩阵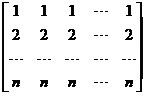 的特征值为
的特征值为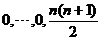 ,从而A的特征值为a,a,
,从而A的特征值为a,a,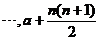 , 故行列式
, 故行列式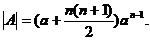
(21)(本题满分9分)
设矩阵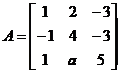 的特征方程有一个二重根,求a的值,并讨论A是否可相似对角化.
的特征方程有一个二重根,求a的值,并讨论A是否可相似对角化.
【分析】 先求出A的特征值,再根据其二重根是否有两个线性无关的特征向量,确定A是否可相似对角化即可.
【详解】 A的特征多项式为
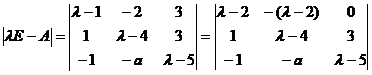
=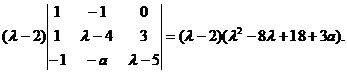
当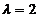 是特征方程的二重根,则有
是特征方程的二重根,则有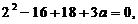 解得a= -2.
解得a= -2.
当a= -2时,A的特征值为2,2,6, 矩阵2E-A=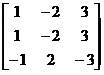 的秩为1,故
的秩为1,故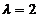 对应的线性无关的特征向量有两个,从而A可相似对角化.
对应的线性无关的特征向量有两个,从而A可相似对角化.
若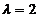 不是特征方程的二重根,则
不是特征方程的二重根,则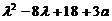 为完全平方,从而18+3a=16,解得
为完全平方,从而18+3a=16,解得 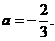
当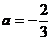 时,A的特征值为2,4,4,矩阵4E-A=
时,A的特征值为2,4,4,矩阵4E-A=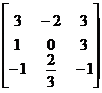 秩为2,故
秩为2,故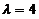 对应的线性无关的特征向量只有一个,从而A不可相似对角化.
对应的线性无关的特征向量只有一个,从而A不可相似对角化.
【评注】 n阶矩阵A可对角化的充要条件是:对于A的任意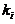 重特征根
重特征根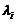 ,恒有
,恒有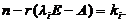 而单根一定只有一个线性无关的特征向量.
而单根一定只有一个线性无关的特征向量.
(22)(本题满分9分)
设A,B为随机事件,且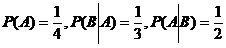 ,令
,令
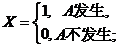
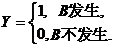
求:(I)二维随机变量(X,Y)的概率分布;
(II)X和Y的相关系数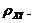
【分析】 先确定(X,Y)的可能取值,再求在每一个可能取值点上的概率,而这可利用随机事件的运算性质得到,即得二维随机变量(X,Y)的概率分布;利用联合概率分布可求出边缘概率分布,进而可计算出相关系数.
【详解】 (I) 由于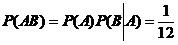 ,
,
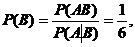
所以, 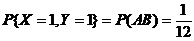 ,
,
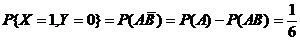 ,
,
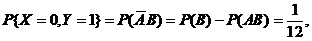
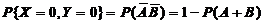
=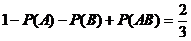
(或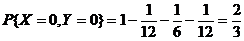 ),
),
故(X,Y)的概率分布为
Y
X 0 1
0 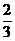
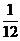
1 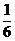
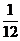
(II) X, Y的概率分布分别为
X 0 1 Y 0 1
P 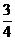
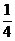 P
P 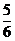
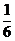
则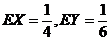 ,
,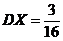 ,DY=
,DY=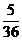 , E(XY)=
, E(XY)=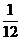 ,
,
故 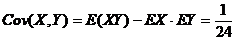 ,从而
,从而
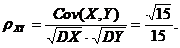
【评注】 本题尽管难度不大,但考察的知识点很多,综合性较强.通过随机事件定义随机变量或通过随机变量定义随机事件,可以比较好地将概率论的知识前后连贯起来,这种命题方式值得注意.
(23)(本题满分9分)
设总体X的分布函数为
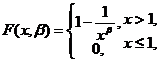
其中未知参数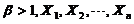 为来自总体X的简单随机样本,求:
为来自总体X的简单随机样本,求:
(I) 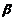 的矩估计量;
的矩估计量;
(II) 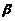 的最大似然估计量.
的最大似然估计量.
【分析】 先由分布函数求出概率密度,再根据求矩估计量和最大似然估计量的标准方法进行讨论即可.
【详解】 X的概率密度为
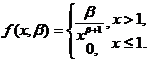
(I) 由于
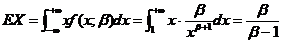 ,
,
令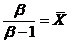 ,解得
,解得 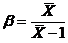 ,所以参数
,所以参数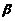 的矩估计量为
的矩估计量为
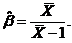
(II)似然函数为
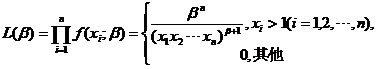
当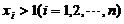 时,
时,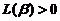 ,取对数得
,取对数得
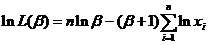 ,
,
两边对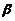 求导,得
求导,得
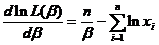 ,
,
令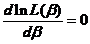 ,可得
,可得 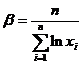 ,
,
故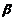 的最大似然估计量为
的最大似然估计量为
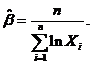
【评注】 本题是基础题型,难度不大,但计算量比较大,实际做题时应特别注意计算的准确性.