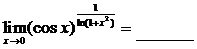
2003考研数学一真题及答案
一、填空题:本题共6小题,每小题4分,共24分,请将答案写在答题纸指定位置上.
(1) 
(2) 曲面 与平面
与平面 平行的切平面的方程是
平行的切平面的方程是 .
.
(3) 设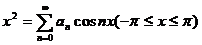 ,则
,则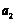 = .
= .
(4) 从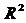 的基
的基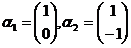 到基
到基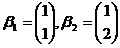 的过渡矩阵为
的过渡矩阵为 .
.
(5) 设二维随机变量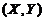 的概率密度为
的概率密度为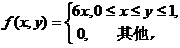 则
则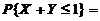
 .
.
(6) 已知一批零件的长度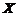 (单位:
(单位: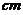 cm)服从正态分布
cm)服从正态分布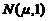 ,从中随机地抽取16个
,从中随机地抽取16个
零件,得到长度的平均值为40 (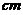 ),则
),则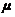 的置信度为0.95的置信区间是
的置信度为0.95的置信区间是 .
.
(注:标准正态分布函数值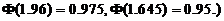
二、选择题:本题共6小题,每小题4分,共24分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.
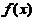 在
在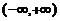 内连续,其导函数的图形如图所示,
内连续,其导函数的图形如图所示,则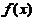 有( )
有( )
(A)一个极小值点和两个极大值点.
(B)两个极小值点和一个极大值点.
(D)三个极小值点和一个极大值点.
(2) 设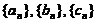 均为非负数列,且
均为非负数列,且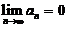 ,
,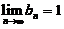 ,
,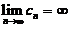 ,则必有( )
,则必有( )
(A) 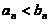 对任意
对任意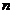 成立. (B)
成立. (B) 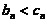 对任意
对任意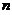 成立.
成立.
(C) 极限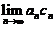 不存在. (D) 极限
不存在. (D) 极限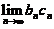 不存在.
不存在.
(3) 已知函数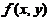 在点
在点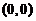 的某个邻域内连续,且
的某个邻域内连续,且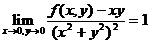 ,则( )
,则( )
(A) 点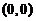 不是
不是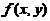 的极值点.
的极值点.
(B) 点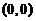 是
是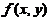 的极大值点.
的极大值点.
(C) 点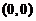 是
是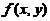 的极小值点.
的极小值点.
(D) 根据所给条件无法判断点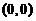 是否为
是否为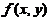 的极值点.
的极值点.
(4) 设向量组I: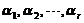 可由向量组II:
可由向量组II: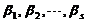 线性表示,则( )
线性表示,则( )
(A) 当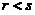 时,向量组II必线性相关. (B) 当
时,向量组II必线性相关. (B) 当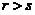 时,向量组II必线性相关.
时,向量组II必线性相关.
(C) 当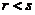 时,向量组I必线性相关. (D) 当
时,向量组I必线性相关. (D) 当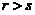 时,向量组I必线性相关.
时,向量组I必线性相关.
(5) 设有齐次线性方程组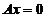 和
和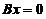 , 其中
, 其中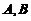 均为
均为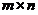 矩阵,现有4个命题:
矩阵,现有4个命题:
① 若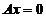 的解均是
的解均是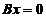 的解,则秩(
的解,则秩(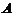 )
)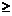 秩(
秩(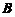 );
);
② 若秩(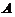 )
)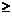 秩(
秩(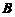 ),则
),则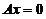 的解均是
的解均是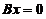 的解;
的解;
③ 若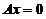 与
与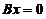 同解,则秩(
同解,则秩(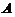 )=秩(
)=秩(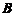 );
);
④ 若秩(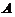 )=秩(
)=秩(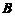 ), 则
), 则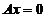 与
与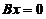 同解.
同解.
以上命题中正确的是( )
(A) ① ②. (B) ① ③.
(C) ② ④. (D) ③ ④.
(6) 设随机变量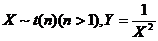 ,则( )
,则( )
(A) 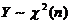 . (B)
. (B) 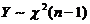 .
.
(C) 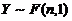 . (D)
. (D) 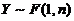 .
.
三 、(本题满分10分)
过坐标原点作曲线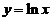 的切线,该切线与曲线
的切线,该切线与曲线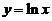 及
及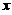 轴围成平面图形
轴围成平面图形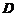 .
.
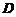 的面积
的面积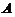 ;
;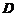 绕直线
绕直线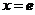 旋转一周所得旋转体的体积
旋转一周所得旋转体的体积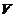 .
.
四 、(本题满分12分)
将函数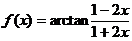 展开成
展开成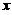 的幂级数,并求级数
的幂级数,并求级数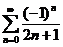 的和.
的和.
五 、(本题满分10分)
已知平面区域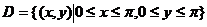 ,
,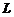 为
为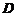 的正向边界. 试证:
的正向边界. 试证:
(1) 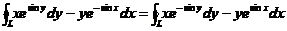 ;
;
(2) 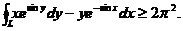
六 、(本题满分10分)
某建筑工程打地基时,需用汽锤将桩打进土层. 汽锤每次击打,都将克服土层对桩的阻力而作功. 设土层对桩的阻力的大小与桩被打进地下的深度成正比(比例系数为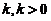 ).汽锤第一次击打将桩打进地下
).汽锤第一次击打将桩打进地下
 . 根据设计方案,要求汽锤每次击打桩时所作的功与前一次击打时所作的功之比为常数
. 根据设计方案,要求汽锤每次击打桩时所作的功与前一次击打时所作的功之比为常数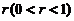 . 问
. 问
(1) 汽锤击打桩3次后,可将桩打进地下多深?
(2) 若击打次数不限,汽锤至多能将桩打进地下多深?
(注: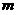 表示长度单位米.)
表示长度单位米.)
七 、(本题满分12分)
设函数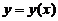 )在
)在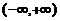 内具有二阶导数,且
内具有二阶导数,且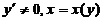 是
是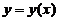 的反函数.
的反函数.
(1) 试将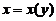 所满足的微分方程
所满足的微分方程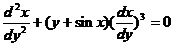 变换为
变换为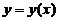 满足的微分方程;
满足的微分方程;
(2) 求变换后的微分方程满足初始条件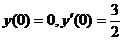 的解.
的解.
八 、(本题满分12分)
设函数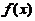 连续且恒大于零,
连续且恒大于零,
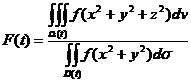 ,
,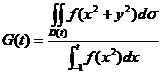 ,
,
其中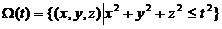 ,
,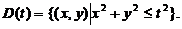
(1) 讨论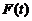 在区间
在区间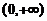 内的单调性.
内的单调性.
(2) 证明当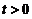 时,
时,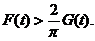
九 、(本题满分10分)
设矩阵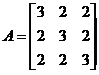 ,
,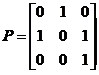 ,
,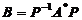 ,求
,求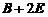 的特征值与特征向量,其中
的特征值与特征向量,其中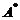 为
为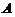 的伴随矩阵,
的伴随矩阵,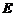 为3阶单位矩阵.
为3阶单位矩阵.
十 、(本题满分8分)
已知平面上三条不同直线的方程分别为
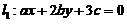 ,
,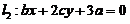 ,
,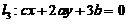 .
.
试证: 这三条直线交于一点的充分必要条件为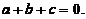
十一 、(本题满分10分)
已知甲、乙两箱中装有同种产品,其中甲箱中装有3件合格品和3件次品,乙箱中仅装有3件合格品. 从甲箱中任取3件产品放入乙箱后,求:
(1) 乙箱中次品件数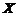 的数学期望;
的数学期望;
(2) 从乙箱中任取一件产品是次品的概率.
十二 、(本题满分8分)
设总体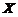 的概率密度为
的概率密度为
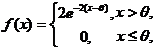
其中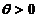 是未知参数. 从总体
是未知参数. 从总体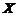 中抽取简单随机样本
中抽取简单随机样本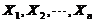 ,记
,记
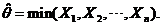
(1) 求总体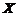 的分布函数
的分布函数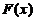 ;
;
(2) 求统计量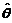 的分布函数
的分布函数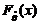 ;
;
(3) 如果用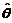 作为
作为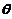 的估计量,讨论它是否具有无偏性.
的估计量,讨论它是否具有无偏性.
参考答案
一、填空题
(1)【答案】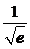
【详解】方法1:求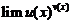 型极限,一般先化为指数形式
型极限,一般先化为指数形式
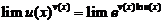

然后求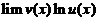 ,再回到指数上去.
,再回到指数上去.
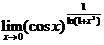 =
=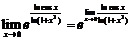 ,
,
而
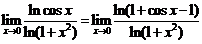
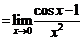 (等价无穷小替换
(等价无穷小替换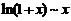 )
)
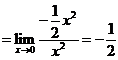 (等价无穷小替换
(等价无穷小替换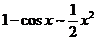 )
)
故 原式=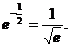
方法2:令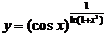 ,有
,有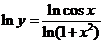 ,以下同方法1.
,以下同方法1.
(2)【答案】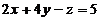
【详解】由题意,只要满足所求切平面的法向量与已知平面的法向量平行即可.
平面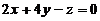 的法向量:
的法向量: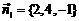 ;
;
曲面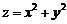 在点
在点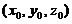 的法向量:
的法向量: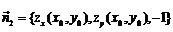
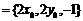
由于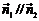 ,因此有
,因此有
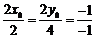
可解得,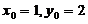 ,相应地有
,相应地有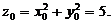
所求切平面过点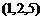 ,法向量为:
,法向量为: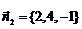 ,故所求的切平面方程为
,故所求的切平面方程为
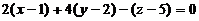 ,即
,即 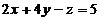
(3)【答案】1
【详解】将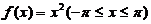 展开为余弦级数
展开为余弦级数
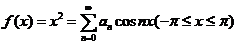 ,其中
,其中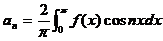 .
.
所以 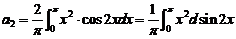
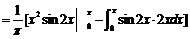
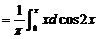
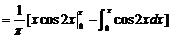
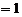
(4)【答案】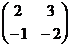
【详解】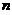 维向量空间中,从基
维向量空间中,从基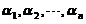 到基
到基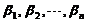 的过渡矩阵
的过渡矩阵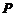 满足
满足
[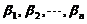 ]=[
]=[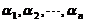 ]
]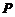 ,
,
因此过渡矩阵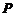 为:
为:
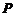 =[
=[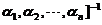 [
[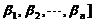 .
.
根据定义,从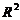 的基
的基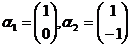 到基
到基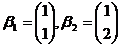 的过渡矩阵为
的过渡矩阵为
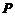 =[
=[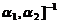 [
[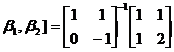 =
=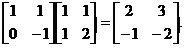
(5)【答案】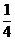 .
.
【分析】本题为已知二维随机变量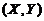 的概率密度
的概率密度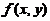 ,求满足一定条件的概率
,求满足一定条件的概率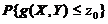 .连续型二维随机变量
.连续型二维随机变量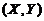 概率的求解方法
概率的求解方法
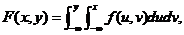
此题可转化为二重积分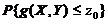
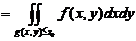 进行计算.
进行计算.
【详解】图中阴影区域为积分区域. 由题设,有
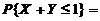
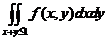
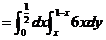
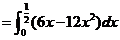
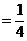
(6)【答案】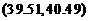 .
.
【分析】可以用两种方法求解:
(1) 已知方差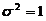 ,对正态总体的数学期望
,对正态总体的数学期望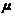 进行估计. 因为
进行估计. 因为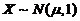 ,设有
,设有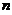 个样本,样本均值
个样本,样本均值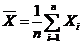 ,则
,则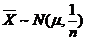 ,将其标准化,由公式
,将其标准化,由公式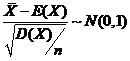 得:
得: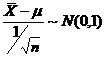
由正态分布分为点的定义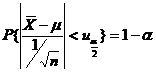 可确定临界值
可确定临界值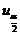 ,进而确定相应的置信区间
,进而确定相应的置信区间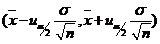 .
.
(2)本题是在单个正态总体方差已知条件下,求期望值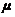 的置信区间问题.由教材上已经求出的置信区间
的置信区间问题.由教材上已经求出的置信区间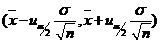 ,其中
,其中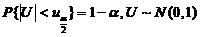 ,可以直接得出答案.
,可以直接得出答案.
【详解】方法1:由题设,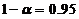 ,可见
,可见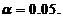 查标准正态分布表知分位点
查标准正态分布表知分位点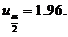 本题
本题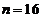 ,
, 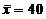 .
.
根据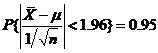 ,有
,有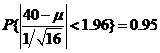 ,
,
即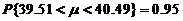 ,故
,故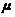 的置信度为0.95的置信区间是
的置信度为0.95的置信区间是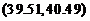 .
.
方法2:由题设,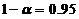 ,
,
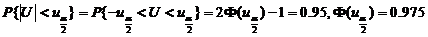
查得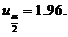 将
将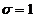 ,
,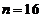 ,
, 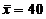 代入
代入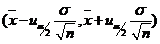 得置信区间
得置信区间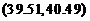
二、选择题
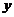
【分析】函数的极值点可能是驻点(一阶导数为零)
或导数不存在的点,极值点是极大值点还是极小值
点可进一步由取极值的第一或第二充分条件判定.
【详解】根据导函数的图形可知,一阶导数为零的
点有3个(导函数与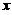 轴交点的个数);
轴交点的个数);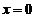 是导数
是导数
不存在的点.
对3个一阶导数为零的点左右两侧导数符号均
不一致,故必为极值点,其中第一个交点左右两侧
导数符号由正变为负,是极大值点;第二个交点和第三个交点左右两侧导数符号由负变为正,是极小值点,则三个驻点中有两个极小值点,一个极大值点;
对导数不存在的点: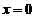 .左侧一阶导数为正,右侧一阶导数为负,可见
.左侧一阶导数为正,右侧一阶导数为负,可见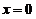 为极大值点.
为极大值点.
故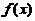 共有两个极小值点和两个极大值点,应选(C).
共有两个极小值点和两个极大值点,应选(C).
(2)【答案】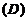
【详解】方法1:推理法
由题设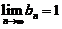 ,假设
,假设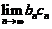 存在并记为
存在并记为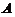 ,则
,则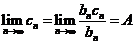 ,这与
,这与 矛盾,故假设不成立,
矛盾,故假设不成立,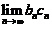 不存在. 所以选项
不存在. 所以选项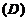 正确.
正确.
方法2:排除法
取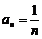 ,
,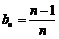 ,满足
,满足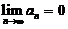 ,
,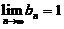 , 而
, 而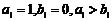 ,
,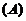 不正确;
不正确;
取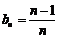 ,
,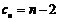 ,满足
,满足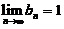 ,
,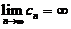 ,而
,而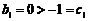 ,
,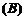 不正确;
不正确;
取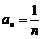 ,
,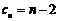 ,满足
,满足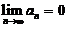 ,
,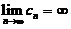 ,而
,而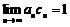 ,
,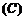 不正确.
不正确.
(3)【答案】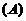
【详解】由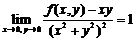
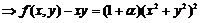 ,其中
,其中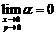 .
.
由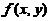 在点
在点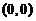 连续知,
连续知,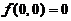 .
.
取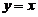 ,
,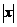 充分小,
充分小,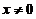 ,有
,有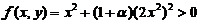 ;
;
取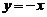 ,
,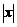 充分小,
充分小,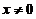 ,有
,有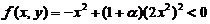
故点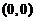 不是
不是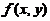 的极值点,应选
的极值点,应选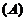 . (极值的定义)
. (极值的定义)
(4)【分析】 本题为一般教材上均有的比较两组向量个数的定理:若向量组I: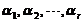 可由向量组II:
可由向量组II: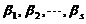 线性表示,则当
线性表示,则当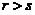 时,向量组I必线性相关. 或其逆否命题:若向量组I:
时,向量组I必线性相关. 或其逆否命题:若向量组I: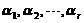 可由向量组II:
可由向量组II: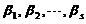 线性表示,且向量组I线性无关,则必有
线性表示,且向量组I线性无关,则必有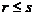 . 可见正确选项为(D). 本题也可通过举反例用排除法找到答案.
. 可见正确选项为(D). 本题也可通过举反例用排除法找到答案.
【详解】 用排除法:
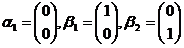 ,则
,则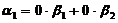 ,但
,但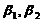 线性无关,排除(A);
线性无关,排除(A);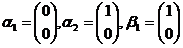 ,则
,则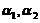 可由
可由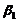 线性表示,但
线性表示,但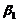 线性无关,排除(B);
线性无关,排除(B);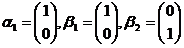 ,
,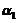 可由
可由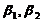 线性表示,但
线性表示,但 线性无关,排除(C).
线性无关,排除(C).
(5)【答案】(B)
【分析】本题可找反例用排除法进行分析,但①、②两个命题的反例比较复杂一些,关键是抓住③、④,迅速排除不正确的选项.
【详解】若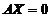 与
与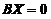 同解,则它们的解空间中的基础解系所含向量个数相同,即
同解,则它们的解空间中的基础解系所含向量个数相同,即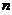 -秩(
-秩(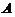 )=
)=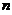 -秩(
-秩(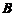 ), 得秩(
), 得秩(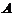 )=秩(
)=秩(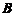 ),命题③成立,可排除(A), (C);
),命题③成立,可排除(A), (C);
但反过来,若秩(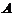 )=秩(
)=秩(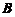 ),则不能推出
),则不能推出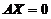 与
与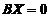 同解,通过举一反例证明,若
同解,通过举一反例证明,若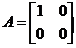 ,
,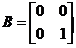 ,则秩(
,则秩(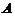 )=秩(
)=秩(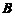 )=1,但
)=1,但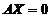 与
与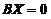 不同解,可见命题④不成立,排除(D). 故正确选项为(B).
不同解,可见命题④不成立,排除(D). 故正确选项为(B).
(6)【答案】(C).
【分析】求解这类问题关键在于了解产生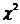 变量、
变量、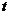 变量、
变量、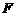 变量的典型模式.
变量的典型模式.
(1)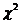 分布:设
分布:设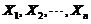 相互独立且均服从标准正态分布,则随机变量
相互独立且均服从标准正态分布,则随机变量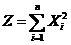 服从自由度为
服从自由度为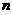 的
的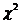 分布.记做
分布.记做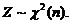
(2)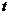 分布:设
分布:设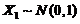 ,
,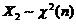 ,且
,且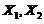 相互独立,则随机变量
相互独立,则随机变量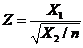 服从自由度为
服从自由度为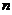 的
的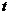 分布.记做
分布.记做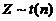
(3)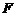 分布:设
分布:设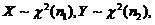 且
且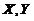 相互独立,则随机变量
相互独立,则随机变量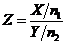 服从
服从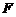 分布,其第一、二自由度分别为
分布,其第一、二自由度分别为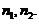 记做
记做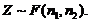
【详解】其实,由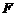 分布的性质以及
分布的性质以及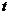 分布和
分布和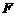 分布的关系得,
分布的关系得,
(1) 如果统计量 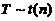 ,则有
,则有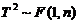 ;
;
(2) 如果统计量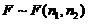 ,则有
,则有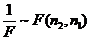 .
.
由以上两条性质可以直接得出本题的答案为(C).
先由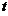 分布的定义知
分布的定义知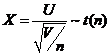 ,其中
,其中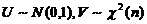 ,于是
,于是
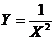 =
=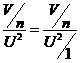 ,
,
分母中只含有一个标准正态分布的平方,所以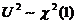 . 由
. 由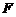 分布的定义知
分布的定义知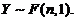 故应选(C).
故应选(C).
三【分析】圆锥体体积公式: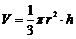 ;旋转体的体积:
;旋转体的体积:
(1) 连续曲线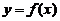 ,直线
,直线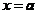 、
、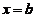 所围成的图形绕直线
所围成的图形绕直线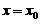 旋转一周而成的立体的体积
旋转一周而成的立体的体积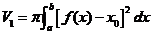
(2) 连续曲线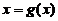 ,直线
,直线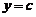 、
、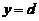 所围成的图形绕直线
所围成的图形绕直线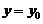 旋转一周而成的立体的体积
旋转一周而成的立体的体积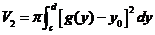
【详解】为了求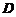 的面积,首先要求出切点的坐标,设切点的横坐标为
的面积,首先要求出切点的坐标,设切点的横坐标为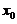 ,则曲线
,则曲线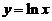 在点
在点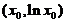 处的切线方程是:
处的切线方程是:
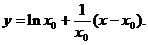
切线的斜率为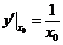 ,由于该切线过原点,将
,由于该切线过原点,将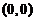 点代入切线方程,得
点代入切线方程,得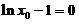 ,从而
,从而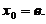 所以该切线的方程为
所以该切线的方程为
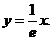
(1) 利用平面图形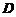 的面积公式
的面积公式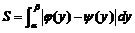 ,得
,得
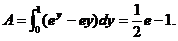
(2) 旋转体体积可用一大立体(圆锥)体积减去一小立体体积进行计算,为了帮助理解,可画一草图.
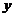
1
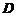
O 1 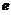
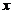
切线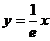 与
与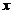 轴及直线
轴及直线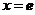 所围成的三角形绕直线
所围成的三角形绕直线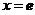 旋转所得的圆锥体积为:
旋转所得的圆锥体积为:
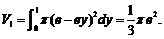
曲线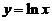 与
与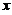 轴及直线
轴及直线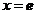 所围成的图形绕直线
所围成的图形绕直线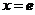 旋转所得的旋转体体积为:
旋转所得的旋转体体积为:
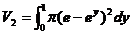
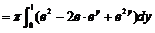
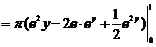
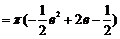
因此所求旋转体的体积为
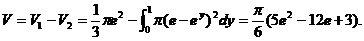
四【分析】幂级数展开有直接法与间接法,一般考查间接法展开,即通过适当的恒等变形、求导或积分等,转化为可利用已知幂级数展开的情形.
另外,由于函数展开成的幂级数,经两边求导或积分(其中一边是逐项求导或逐项积分)后,其新的展开式收敛区间不变,但在收敛区间端点处,求导(积分)后的展开式成立与否,要另行单独处理,设已有
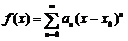
收敛区间为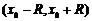 . 如果在
. 如果在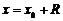 处级数收敛,并且
处级数收敛,并且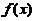 (左)连续,则展开式成立的范围可扩大到
(左)连续,则展开式成立的范围可扩大到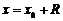 处,在
处,在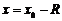 处亦有类似的结论,不过此时
处亦有类似的结论,不过此时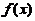 (左)连续应改称(右)连续.
(左)连续应改称(右)连续.
【详解】本题可先求导,
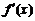
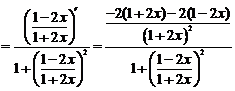 基本求导公式
基本求导公式
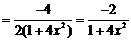
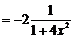
对于函数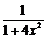 ,可以利用我们所熟悉的函数
,可以利用我们所熟悉的函数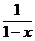 的幂级数展开:
的幂级数展开:
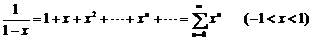
所以 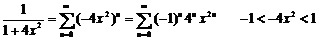 (把
(把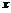 换成
换成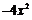 )
)
有 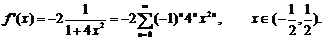
对上式两边求积分,得
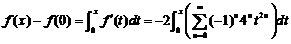
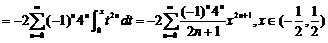 ,
,
又因为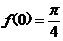 ,所以
,所以
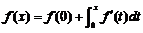 =
=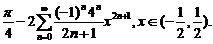
即 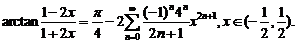 (*)
(*)
在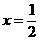 处,右边级数成为
处,右边级数成为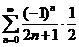 ,收敛(利用莱布尼茨定理),左边函数
,收敛(利用莱布尼茨定理),左边函数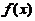 连续,所以成立范围可扩大到
连续,所以成立范围可扩大到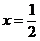 处.而在
处.而在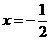 处,右边级数虽然收敛,但左边函数
处,右边级数虽然收敛,但左边函数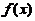 不连续,所以成立范围只能是
不连续,所以成立范围只能是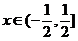 .
.
为了求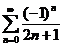 ,令
,令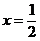 代入(*)得
代入(*)得
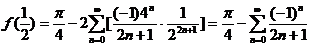 ,
,
再由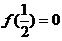 ,得
,得
五【详解】(1) 方法1:用格林公式证明. 由曲线为正向封闭曲线,自然想到用格林公式
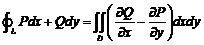 .
.
所以 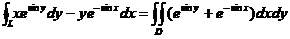
所以 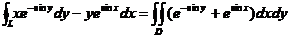
因为积分区域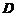 关于
关于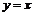 对称,所以
对称,所以
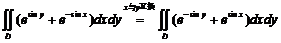
故 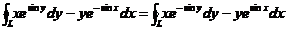
方法2:化为定积分证明
左边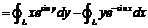 =
=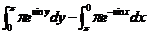 =
=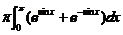
右边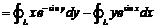 =
=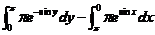 =
=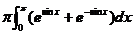
所以 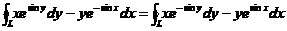 .
.
(2) 方法1:用格林公式证明
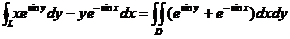
=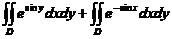 =
=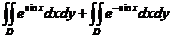 利用轮换对称性
利用轮换对称性
=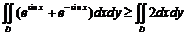
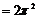
(因为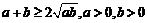 )
)
方法2:由(1)知,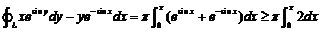
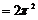
六【详解】(1) 建立坐标系,地面作为坐标原点,向下为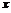 轴正向,设第
轴正向,设第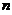 次击打后,桩被打进地下
次击打后,桩被打进地下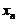 ,第
,第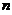 次击打时,汽锤所作的功为
次击打时,汽锤所作的功为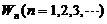 .由题设,当桩被打进地下的深度为
.由题设,当桩被打进地下的深度为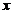 时,土层对桩的阻力的大小为
时,土层对桩的阻力的大小为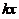 ,汽锤所作的功等于克服阻力所做的功.
,汽锤所作的功等于克服阻力所做的功.
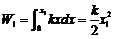 ,
,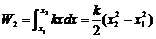 ,
,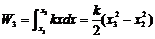 ,
,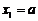
从而 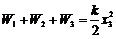
又 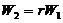 ,
,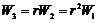 ,
,
从而 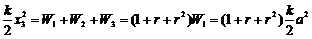
于是 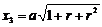 .
.
(2) 第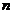 次击打后,桩被打进地下
次击打后,桩被打进地下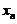 ,第
,第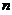 次击打时,汽锤所作的功为
次击打时,汽锤所作的功为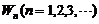 .
.
则汽锤前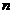 次所功的和等于克服桩被打进地下
次所功的和等于克服桩被打进地下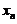
 所做的功.
所做的功.
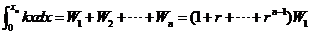
而 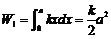 牛-莱公式
牛-莱公式
所以 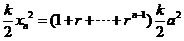
从而 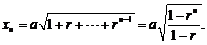 等比数列求和公式
等比数列求和公式
由于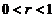 ,所以
,所以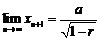 .
.
七【详解】 (1) 将题中的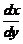 与
与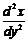 变换成以
变换成以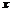 为自变量
为自变量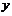 为因变量的导数
为因变量的导数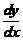 与
与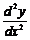 来表示(即通常所说的反函数变量变换),有
来表示(即通常所说的反函数变量变换),有
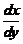 =
=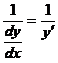 ,
,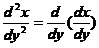 =
=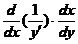 =
=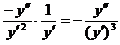 .
.
代入原方程,得 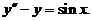 ( * )
( * )
(2) 方程( * )所对应的齐次方程为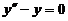 ,特征方程为
,特征方程为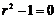 ,根
,根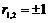 ,因此通解为
,因此通解为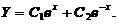 由于
由于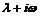 不是特征方程得根,所以设方程( * )的特解为
不是特征方程得根,所以设方程( * )的特解为
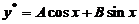
则 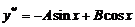 ,
,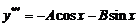
代入方程( * ),得: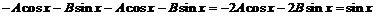
解得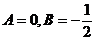 ,故
,故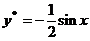 . 从而
. 从而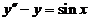 的通解为
的通解为
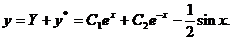
由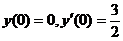 ,得
,得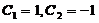 .故变换后的微分方程满足初始条件
.故变换后的微分方程满足初始条件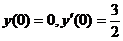 的解为
的解为
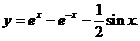
且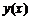 的导函数
的导函数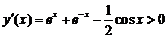 ,满足题设
,满足题设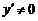 条件.
条件.
八【详解】(1) 首先对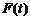 进行化简,三重积分转化为在球面坐标系中的计算;二重积分转化为在极坐标系中的计算.
进行化简,三重积分转化为在球面坐标系中的计算;二重积分转化为在极坐标系中的计算.
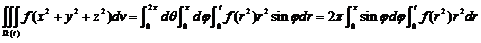
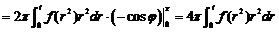 (球面坐标)
(球面坐标)
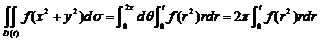 (极坐标)
(极坐标)
所以
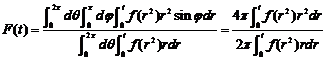
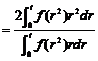
为了讨论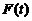 在区间
在区间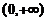 内的单调性,对
内的单调性,对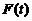 求导:
求导:
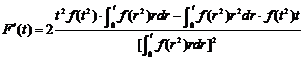
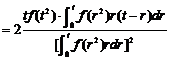
由于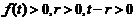 ,所以
,所以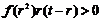 . 再利用定积分的性质:若在区间
. 再利用定积分的性质:若在区间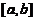 上
上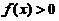 ,则
,则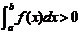 . 所以
. 所以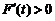 ,所以
,所以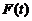 在区间
在区间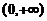 内严格单调增加.
内严格单调增加.
(2) 将待证的不等式作适当的恒等变形后,构造辅助函数,再用单调性进行证明即可.
因为 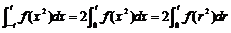 ,
,
所以
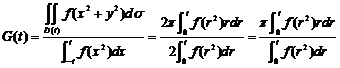
要证明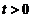 时
时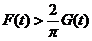 ,只需证明
,只需证明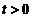 时,
时,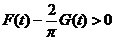 ,即
,即
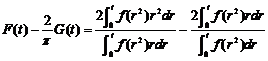
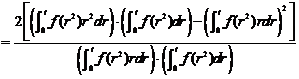
令 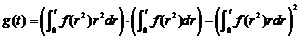
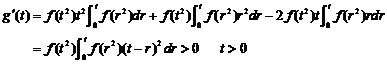
故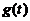 在
在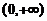 内单调增加,又因为
内单调增加,又因为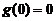 ,所以当
,所以当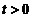 时,有
时,有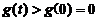 ,
,
从而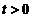 时,
时,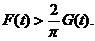
九【分析】 法1:可先求出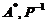 ,进而确定
,进而确定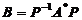 及
及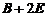 ,再按通常方法确定其特征值和特征向量;法2:先求出
,再按通常方法确定其特征值和特征向量;法2:先求出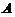 的特征值与特征向量,再相应地确定
的特征值与特征向量,再相应地确定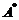 的特征值与特征向量,最终根据
的特征值与特征向量,最终根据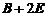 与
与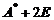 相似求出其特征值与特征向量.
相似求出其特征值与特征向量.
【详解】方法1:经计算可得
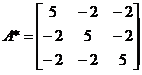 ,
,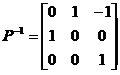 ,
,
所以 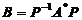 =
=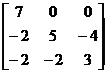 ,
,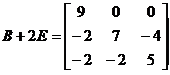 .
.
令 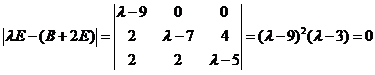 ,
,
故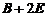 的特征值为
的特征值为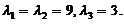
当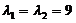 时,解
时,解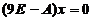 ,得线性无关的特征向量为
,得线性无关的特征向量为
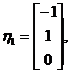
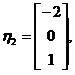
所以属于特征值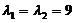 的所有特征向量为
的所有特征向量为
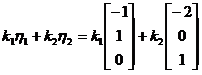 ,其中
,其中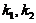 是不全为零的任意常数.
是不全为零的任意常数.
当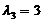 时,解
时,解 ,得线性无关的特征向量为
,得线性无关的特征向量为
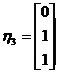 ,
,
所以属于特征值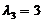 的所有特征向量为
的所有特征向量为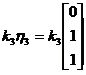 ,其中
,其中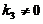 为任意常数.
为任意常数.
方法2:设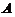 的特征值为
的特征值为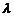 ,对应的特征向量为
,对应的特征向量为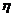 ,即
,即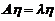 .由于
.由于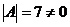 ,所以
,所以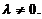
所以 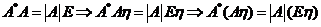
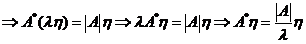 ,
,
于是 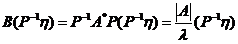 ,
,
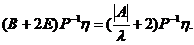
因此,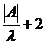 为
为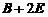 的特征值,对应的特征向量为
的特征值,对应的特征向量为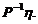
由于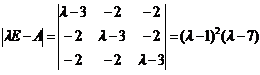 ,故
,故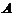 的特征值为
的特征值为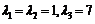
当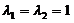 时,对应的线性无关特征向量可取为
时,对应的线性无关特征向量可取为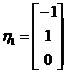 ,
, 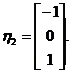
当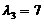 时,对应的一个特征向量为
时,对应的一个特征向量为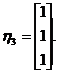
由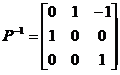 ,得
,得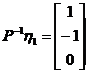 ,
,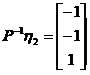 ,
,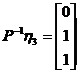 .
.
因此,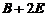 的三个特征值分别为9,9,3.对应于特征值9的全部特征向量为
的三个特征值分别为9,9,3.对应于特征值9的全部特征向量为
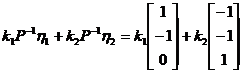 ,其中
,其中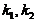 是不全为零的任意常数;
是不全为零的任意常数;
对应于特征值3的全部特征向量为
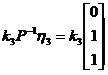 ,其中
,其中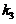 是不为零的任意常数.
是不为零的任意常数.
十【分析】三条直线相交于一点,相当于对应线性方程组有唯一解,进而转化为系数矩阵与增广矩阵的秩均为2.
【详解】方法1:“必要性”. 设三条直线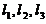 交于一点,则线性方程组
交于一点,则线性方程组
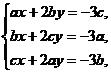 (*)
(*)
有唯一解,故系数矩阵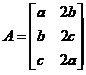 与增广矩阵
与增广矩阵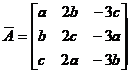 的秩均为2,于是
的秩均为2,于是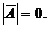
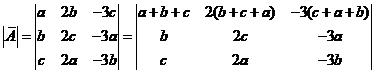
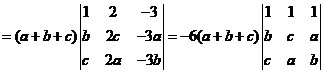
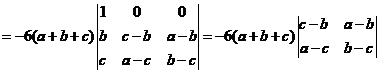
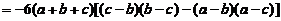
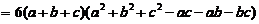
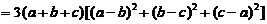 ,
,
由于三条直线互不相同,所以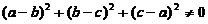 ,故
,故
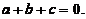
“充分性”. 由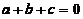 ,则从必要性的证明可知,
,则从必要性的证明可知,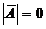 ,故秩
,故秩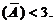
由于
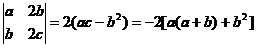 =
=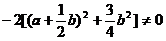 ,
,
故秩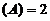 .于是,秩(
.于是,秩(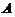 )=秩
)=秩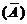 =2.因此方程组(*)有唯一解,即三直线
=2.因此方程组(*)有唯一解,即三直线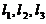 交于一点.
交于一点.
方法2:“必要性”
设三直线交于一点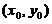 ,则
,则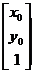 为
为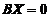 的非零解,其中
的非零解,其中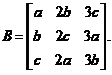
所以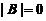 .而
.而
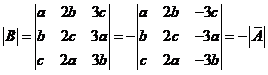
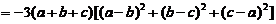 ,(解法同方法1)
,(解法同方法1)
但根据题设 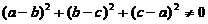 ,故
,故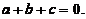
“充分性”:考虑线性方程组
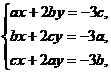 (*)
(*)
将方程组(*)的三个方程相加,并由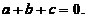 可知,方程组(*)等价于方程组
可知,方程组(*)等价于方程组
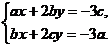 (* *)
(* *)
因为 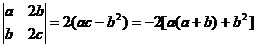 =
=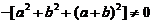 ,
,
故方程组(* *)有唯一解,所以方程组(*)有唯一解,即三直线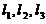 交于一点.
交于一点.
十一【详解】乙箱中可能的次品件数为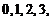 分别求出其概率,再按定义求数学期望即可;而求从乙箱中任取一件产品是次品的概率,涉及到两次试验,是典型的用全概率公式的情形,第一次试验的各种可能结果(取到的次品数)就是要找的完备事件组.
分别求出其概率,再按定义求数学期望即可;而求从乙箱中任取一件产品是次品的概率,涉及到两次试验,是典型的用全概率公式的情形,第一次试验的各种可能结果(取到的次品数)就是要找的完备事件组.
(1) 方法1: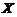 的可能取值为
的可能取值为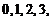 取出
取出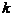 件次品
件次品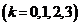 的取法有
的取法有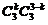 种;
种;
样本空间即从两个箱子中取出3件产品的总的取法数为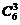 .所以有,
.所以有,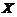 的概率分布为
的概率分布为
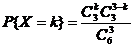 ,
, 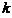
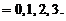
即 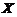 0 1 2 3
0 1 2 3
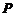
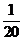
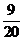
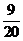
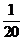
因此,由离散型数学期望的定义
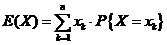
易得 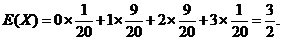
方法2:本题对数学期望的计算也可用分解法:
设
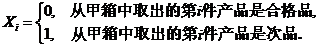
则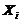 的概率分布为
的概率分布为
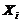 0 1
0 1
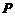
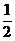
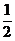
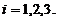
因为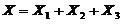 ,所以由数学期望的线性可加性,有
,所以由数学期望的线性可加性,有
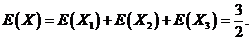
(2) 设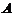 表示事件“从乙箱中任取一件产品是次品”,由于
表示事件“从乙箱中任取一件产品是次品”,由于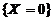 ,
,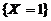 ,
,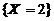 ,
,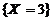 构成完备事件组,因此根据全概率公式,有
构成完备事件组,因此根据全概率公式,有
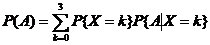 =
=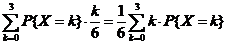
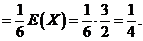
十二【分析】本题表面上是一数理统计问题,实际上考查了求分布函数、随机变量的函数求分布和概率密度以及数学期望的计算等多个知识点.将数理统计的概念与随机变量求分布与数字特征结合起来是一种典型的命题形式.
求分布函数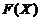 是基本题型:求统计量
是基本题型:求统计量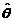 的分布函数
的分布函数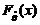 ,可作为多维相互独立且同分布的随机变量函数求分布函数,直接用定义即可;是否具有无偏性,只需检验
,可作为多维相互独立且同分布的随机变量函数求分布函数,直接用定义即可;是否具有无偏性,只需检验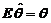 是否成立.
是否成立.
【详解】(1) 由连续型随机变量分布函数的定义,有
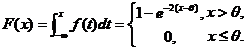
(2) 由题给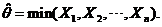 ,有
,有
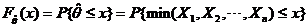
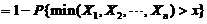
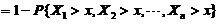
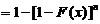
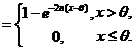
(3) 由连续型随机变量概率密度是分布函数在相应区间上的微分得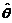 概率密度为
概率密度为
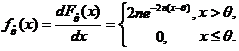
因为 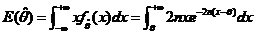
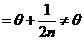 ,
,
所以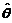 作为
作为 的估计量不具有无偏性.
的估计量不具有无偏性.