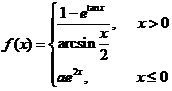 在
在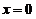 处连续,则
处连续,则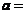 .
.
一、填空题(本题共5小题,每小题3分,满分15分,把答案填在题中横线上)
(1) 设函数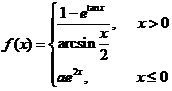 在
在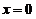 处连续,则
处连续,则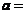 .
.
(2) 位于曲线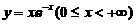 下方,
下方,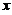 轴上方的无界图形的面积是_______.
轴上方的无界图形的面积是_______.
(3) 微分方程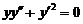 满足初始条件
满足初始条件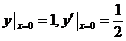 的特解是_________.
的特解是_________.
(4) 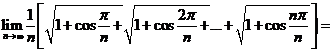 _____ .
_____ .
(5) 矩阵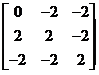 的非零特征值是_________.
的非零特征值是_________.
二、选择题(本题共5小题,每小题3分,共15分,在每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)
(1) 设函数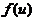 可导,
可导,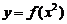 当自变量
当自变量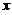 在
在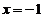 处取得增量
处取得增量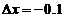 时,相应的函数增量
时,相应的函数增量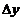 的线性主部为
的线性主部为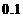 ,则
,则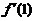 =( )
=( )
(A)-1 (B)0.1 (C)1 (D)0.5
(2) 设函数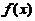 连续,则下列函数中,必为偶函数的是( )
连续,则下列函数中,必为偶函数的是( )
(A)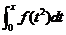 (B)
(B)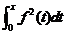
(C)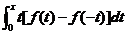 (D)
(D)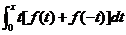
(3) 设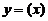 是二阶常系数微分方程
是二阶常系数微分方程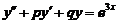 满足初始条
满足初始条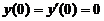 的特解,则当
的特解,则当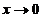 ,函数
,函数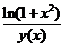 的极限( )
的极限( )
(A)不存在 (B)等于1 (C)等于2 (D)等于3
(4) 设函数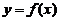 在
在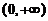 内有界且可导,则( )
内有界且可导,则( )
(A)当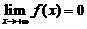 时,必有
时,必有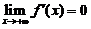 .
.
(B)当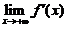 存在时,必有
存在时,必有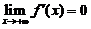 .
.
(C)当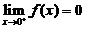 时,必有
时,必有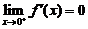 .
.
(D)当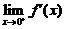 存在时,必有
存在时,必有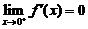 .
.
(5) 设向量组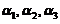 线性无关,向量
线性无关,向量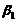 可由
可由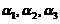 线性表示,而向量
线性表示,而向量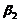 不能由
不能由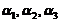 线性表示,则对于任意常数
线性表示,则对于任意常数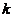 ,必有( )
,必有( )
(A)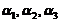 ,
, 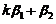 线性无关; (B)
线性无关; (B)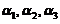 ,
, 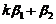 线性相关;
线性相关;
(C)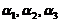 ,
,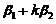 线性无关; (D)
线性无关; (D)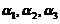 ,
,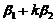 线性相关
线性相关
三、(本题满分6分)
已知曲线的极坐标方程是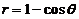 ,求该曲线上对应于
,求该曲线上对应于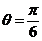 处的切线与法线的直角坐标方程.
处的切线与法线的直角坐标方程.
四、(本题满分7分)
设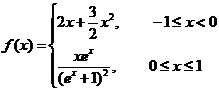 求函数
求函数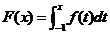 的表达式.
的表达式.
五、(本题满分7分)
已知函数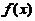 在
在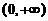 内可导
内可导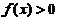 ,
,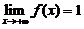 , 且满足
, 且满足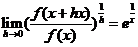 ,求
,求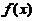 .
.
六、(本题满分8分)
求微分方程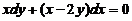 的一个解
的一个解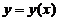 ,使得由曲线
,使得由曲线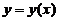 , 与直线
, 与直线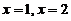 以及
以及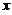 轴所围成的平面图形绕
轴所围成的平面图形绕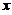 轴旋转一周的旋转体体积最小.
轴旋转一周的旋转体体积最小.
七、(本题满分7分)
某闸门的性状与大小如图所示,其中直线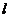 为对
为对
称轴,闸门的上部为矩形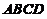 ,下部由二次抛物线
,下部由二次抛物线
与线段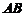 所围成,当水面与闸门的上端相平时,欲使
所围成,当水面与闸门的上端相平时,欲使
闸门矩形部分承受的水压力与闸门下部承受的水压力之
比为5:4,闸门矩形部分的高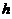 应为多少
应为多少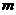 (米)?
(米)?
八、(本题满分8分)
设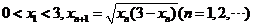 ,证明数列
,证明数列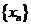 的极限存在,并求此极限.
的极限存在,并求此极限.
九、(本题满分8分)
设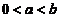 ,证明不等式
,证明不等式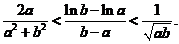
十、(本题满分8分)
设函数 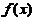 在
在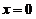 的某邻域内具有二阶连续导数,且
的某邻域内具有二阶连续导数,且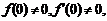
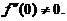
证明:存在惟一的一组实数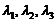 ,使得当
,使得当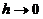 时,
时,
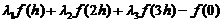
是比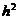 高阶的无穷小.
高阶的无穷小.
十一、(本题满分6分)
已知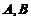 为3 阶矩阵,且满足
为3 阶矩阵,且满足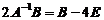 ,其中
,其中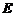 是3阶单位矩阵.
是3阶单位矩阵.
(1) 证明:矩阵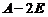 可逆;
可逆;
(2) 若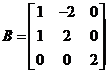 ,求矩阵
,求矩阵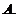
十二、(本题满6分)
已知4阶方阵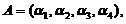
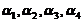 均为4维列向量,其中
均为4维列向量,其中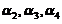 线性无关,
线性无关,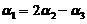 .如果
.如果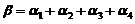 ,求线性方程组
,求线性方程组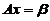 的通解.
的通解.
参考答案
一、填空题
(1)【答案】 -2
【详解】如果分段函数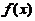 连续,则
连续,则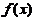 在0点处的左右极限相等,从而确定
在0点处的左右极限相等,从而确定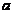 的值.
的值.
当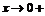 时,
时,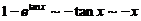 ;
;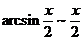 ,所以有
,所以有
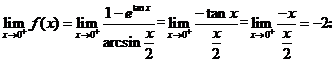
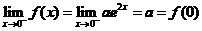
如果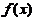 在
在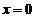 处连续,必有
处连续,必有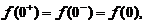 即
即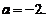
(2)【答案】 1
【详解】面积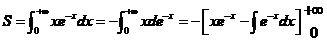
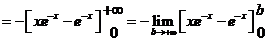
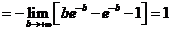
其中 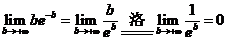 .
.
(3)【答案】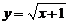
【详解】方法1:这是属于缺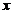 的
的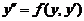 类型. 命
类型. 命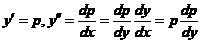 .
.
原方程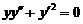 化为
化为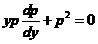 ,得
,得
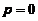 或
或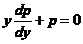
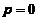 ,即
,即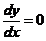 ,不满足初始条件
,不满足初始条件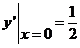 ,弃之;所以
,弃之;所以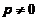
所以,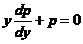 ,分离变量得
,分离变量得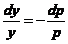 ,解之得
,解之得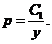 即
即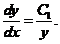
由初始条件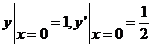 ,可将
,可将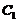 先定出来:
先定出来: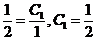 . 于是得
. 于是得
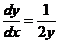
解之得,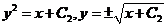 .以
.以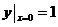 代入,得
代入,得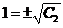 ,所以应取“+”号
,所以应取“+”号
且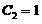 . 于是特解是
. 于是特解是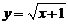 .
.
方法2:将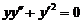 改写为
改写为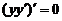 ,从而得
,从而得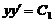 . 以初始条件
. 以初始条件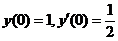 代入,有
代入,有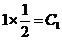 ,所以得
,所以得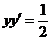 . 即
. 即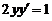 ,改写为
,改写为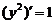 . 解得
. 解得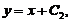
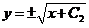 .再以初值代入,
.再以初值代入,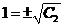 所以应取
所以应取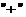 且
且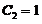 . 于是特解
. 于是特解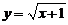 .
.
(4)【答案】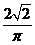
【详解】利用定积分的概念将被积函数化为定积分求极限.
因为 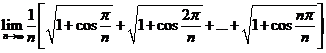
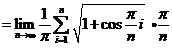
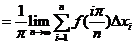
其中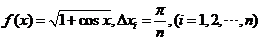 ,所以根据定积分的定义,有
,所以根据定积分的定义,有
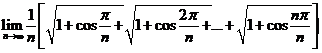
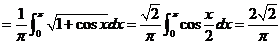
(5)【答案】4
【详解】记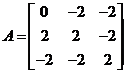 ,则
,则
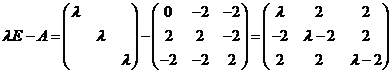 (对应元素相减)
(对应元素相减)
两边取行列式,
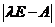
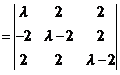
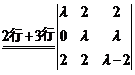
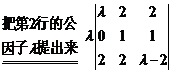
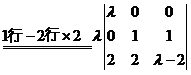
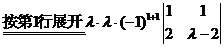
(其中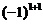 指数中的1和1分别是
指数中的1和1分别是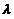 所在的行数和列数)
所在的行数和列数)
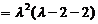
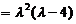
令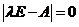 ,解得
,解得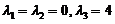 ,故
,故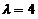 是矩阵的非零特征值.(另一个特征值是
是矩阵的非零特征值.(另一个特征值是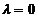 (二重))
(二重))
二、选择题
(1)【答案】(D)
【详解】在可导条件下,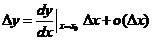 ,当
,当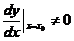 时
时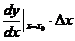 称为
称为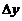 的线性主部.
的线性主部.
而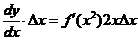 ,以
,以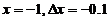 代入得
代入得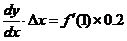 ,由题设它等于0.1,于是
,由题设它等于0.1,于是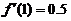 ,应选(D).
,应选(D).
(2)【答案】(D)
【详解】对与(D),令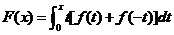 ,则
,则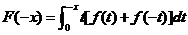 ,令
,令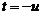 ,则
,则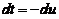 ,所以
,所以
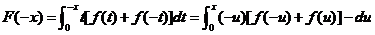
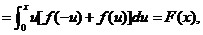
所以(D)为偶函数.同理证得(A)、(C)为奇函数,而(B)不确定,如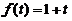 .故应选(D).
.故应选(D).
(3)【答案】(C)
【详解】由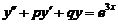 ,且
,且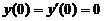 ,可知
,可知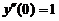
方法1:因为当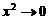 时,
时,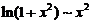 ,所以
,所以
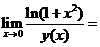
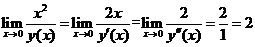 ,
,
故选(C).
方法2:由于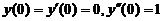 . 将函数
. 将函数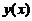 按麦克劳林公式展开
按麦克劳林公式展开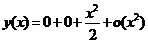 ,代入
,代入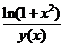 ,有
,有
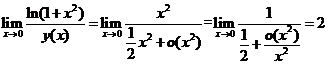 .
.
(4) 【详解】方法1:排斥法.
令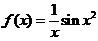 ,则
,则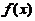 在
在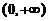 有界,
有界,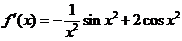 ,
,
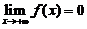 ,但
,但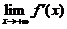 不存在,故(A)不成立;
不存在,故(A)不成立;
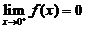 ,但
,但 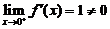 ,(C)和(D)不成立,故选(B).
,(C)和(D)不成立,故选(B).
方法2:证明(B)正确. 设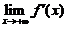 存在,记
存在,记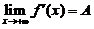 ,证明
,证明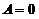 .
.
用反证法,若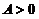 ,则对于
,则对于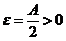 ,存在
,存在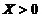 ,使当
,使当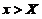 时,
时,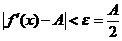 ,即
,即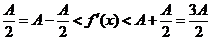
由此可知,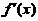 有界且大于
有界且大于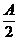 .在区间
.在区间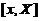 上应用拉格朗日中值定理,有
上应用拉格朗日中值定理,有
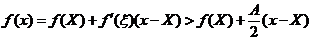
从而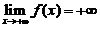 ,与题设
,与题设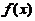 有界矛盾.类似可证当
有界矛盾.类似可证当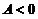 时亦有矛盾. 故
时亦有矛盾. 故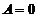 .
.
(5)【答案】A
【详解】方法1:对任意常数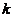 ,向量组
,向量组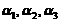 ,
,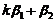 线性无关. 用反证法,若
线性无关. 用反证法,若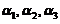 ,
,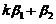 线性相关,因已知
线性相关,因已知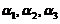 线性无关,故
线性无关,故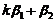 可由
可由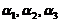 线性表出. 即存在常数
线性表出. 即存在常数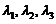 ,使得
,使得 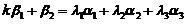
又已知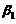 可由
可由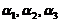 线性表出,即存在常数
线性表出,即存在常数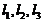 ,使得
,使得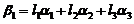 代入上式,得
代入上式,得
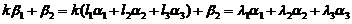
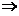
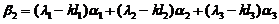
与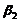 不能由
不能由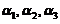 线性表出矛盾.故向量组
线性表出矛盾.故向量组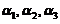 ,
,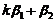 线性无关,选(A)
线性无关,选(A)
方法2:用排除法
B选项:取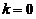 ,向量组
,向量组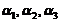 ,
,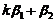 即
即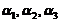 ,
,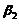 线性相关不成立,否则因为
线性相关不成立,否则因为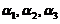 ,
,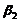 线性相关,又
线性相关,又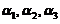 线性无关,故
线性无关,故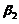 可由
可由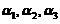 线性表出.即存在常数
线性表出.即存在常数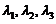 ,使得
,使得 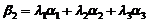 与已知矛盾,排除(B).
与已知矛盾,排除(B).
C选项:取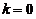 ,向量组
,向量组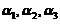 ,
,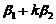 ,即
,即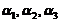 ,
,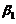 线性无关不成立,因为
线性无关不成立,因为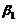 可由
可由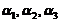 线性表出,
线性表出,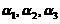 ,
,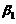 线性相关,排除(C).
线性相关,排除(C).
D选项: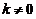 时,
时,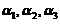 ,
,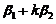 线性相关不成立.若
线性相关不成立.若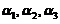 ,
,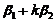 线性相关,因已知
线性相关,因已知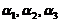 线性无关,故
线性无关,故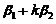 可由
可由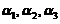 线性表出.即存在常数
线性表出.即存在常数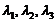 ,使得
,使得 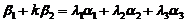 . 又已知
. 又已知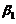 可由
可由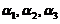 线性表出,即存在常数
线性表出,即存在常数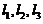 ,使得
,使得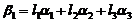 代入上式,得
代入上式,得
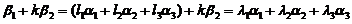
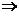
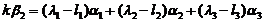
因为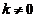 ,故
,故 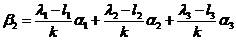
与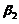 不能由
不能由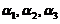 线性表出矛盾.故
线性表出矛盾.故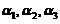 ,
,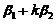 线性相关不成立,排除(D).
线性相关不成立,排除(D).
故选(A).
三【详解】由极坐标到直角坐标的变换公式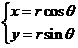 ,化极坐标曲线
,化极坐标曲线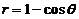 为直角坐标的参数方程为
为直角坐标的参数方程为
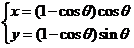 , 即
, 即 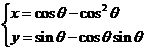
曲线上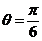 的点对应的直角坐标为
的点对应的直角坐标为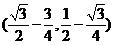
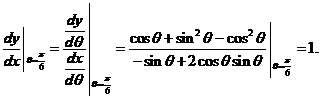
于是得切线的直角坐标方程为
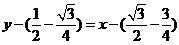 ,即
,即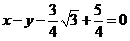 .
.
(这是由直线的点斜式得到的,直线的点斜式方程为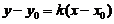 ,由导数的几何意义知在
,由导数的几何意义知在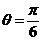 时斜率为1,且该点的直角坐标为
时斜率为1,且该点的直角坐标为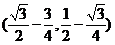 ),
),
法线方程为
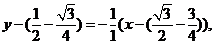 即
即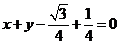 .
.
(这是由直线的点斜式方程及在同一点切线斜率与法线斜率为负倒数的关系而得)
四【详解】当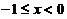 时
时
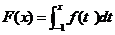
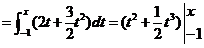
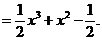
当 时,
时,
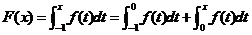
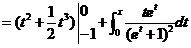
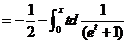
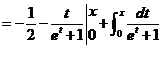
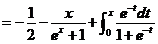
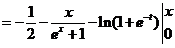
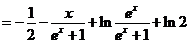
所以
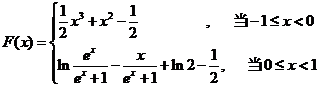
五【详解】因为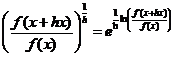 ,
,
又 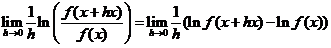 ,
, 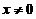
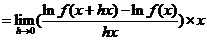
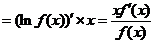
从而得到 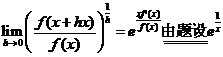
于是推得 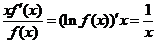 ,即
,即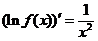
解此微分方程,得 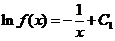 ,改写成
,改写成 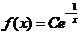
再由条件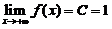 ,于是得
,于是得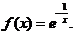
六【详解】这是一阶线性微分方程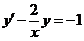 ,由通解公式(如果一个一阶线性方程为
,由通解公式(如果一个一阶线性方程为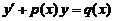 那么通解为
那么通解为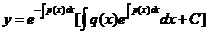 )有
)有
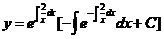
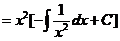
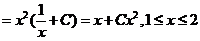
由曲线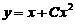 与
与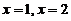 及
及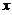 轴围成的图形绕
轴围成的图形绕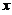 轴旋转一周的旋转体的体积为
轴旋转一周的旋转体的体积为
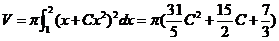
(旋转体的体积公式:设有连续曲线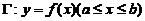 ,
,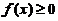 与直线
与直线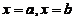 及
及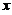 轴围成平面图形.该图形绕
轴围成平面图形.该图形绕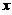 轴旋转一周产生旋转体的体积为
轴旋转一周产生旋转体的体积为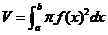 )
)
取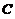 使
使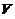 最小,由求最值的方法知先求函数的驻点,即
最小,由求最值的方法知先求函数的驻点,即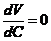 的点,
的点,
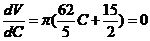
解得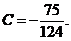 又
又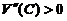 ,故
,故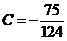 为
为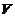 的惟一极小值点,也是最小值点,于是所求曲线为
的惟一极小值点,也是最小值点,于是所求曲线为
y
D 1m 1m C
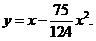
七【详解】方法1:建立坐标系如下图,
由于底部是二次抛物线我们设此抛物线为
l h
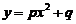 ,由坐标轴的建立知此抛物线过
,由坐标轴的建立知此抛物线过A B
O x
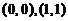 点,把这两点代入抛物线的方程,
点,把这两点代入抛物线的方程,1m
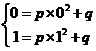 ,所以
,所以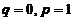 .
.即底部的二次抛物线是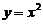 ,
,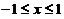 .
.
细横条为面积微元,按所建立的坐标系及抛物线的方程,得到面积微元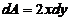 ,因此压力微元
,因此压力微元
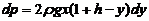 (这是由压力的公式得到的:压力=压强
(这是由压力的公式得到的:压力=压强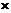 面积)
面积)
平板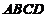 上所受的总压力为
上所受的总压力为
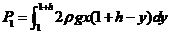
其中以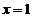 代入,计算得
代入,计算得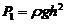 .
.
抛物板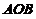 上所受的总压力为
上所受的总压力为
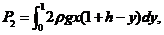
其中由抛物线方程知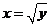 ,代入计算得
,代入计算得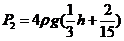 ,
,
由题意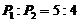 ,即
,即 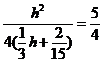
解之得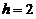 (米)(
(米)(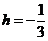 舍去),即闸门矩形部分的高应为
舍去),即闸门矩形部分的高应为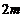 .
.
八【详解】由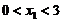 知
知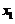 及
及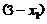 均为正数,故
均为正数,故
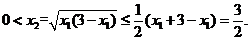 (
(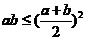
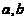 为正数)
为正数)
假设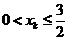 ,则再一次用不等式
,则再一次用不等式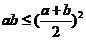 ,得
,得
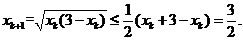
由数学归纳法知,对任意正整数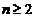 有
有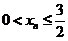 .
.
另一方面,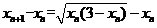
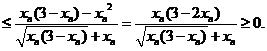
所以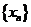 单调增加.单调增加数列
单调增加.单调增加数列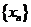 有上界,所以
有上界,所以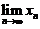 存在,记为
存在,记为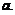
由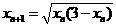 两边取极限,于是由极限的运算性质得
两边取极限,于是由极限的运算性质得
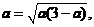 即
即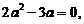
解得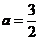 或
或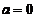 ,但因
,但因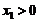 且单调增,故
且单调增,故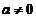 ,所以
,所以
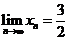 .
.
九【详解】左、右两个不等式分别考虑. 先证左边不等式,
方法1:由所证的形式想到用拉格朗日中值定理.
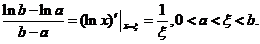
而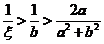 中第二个不等式来自不等式
中第二个不等式来自不等式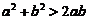 (当
(当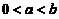 时),这样就证明了要证明的左边.
时),这样就证明了要证明的左边.
方法2:用单调性证,将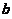 改写为
改写为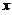 并移项,命
并移项,命
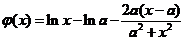 ,有
,有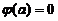 .
.
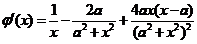
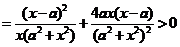 (当
(当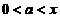 ),
),
所以,当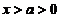 时
时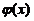 单调递增. 所以
单调递增. 所以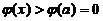 ,故
,故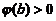 ,
,
即 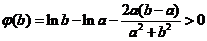
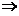
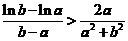
再证右边不等式,用单调性证,将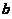 改写为
改写为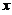 并移项,命
并移项,命
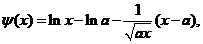
有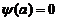 ,及
,及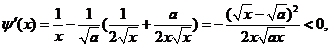
所以当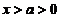 时,
时,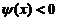 ,再以
,再以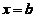 代入,得
代入,得
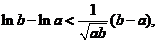 即
即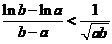 .
.
右边证毕.
十【详解】从题目结论出发,要证存在唯一的一组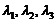 ,使得
,使得
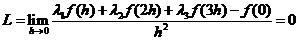
由极限的四则运算法则知,分子极限应为0,即
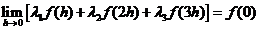
由于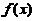 在
在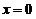 连续,于是上式变形为
连续,于是上式变形为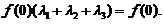 由
由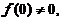 知
知
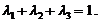 (1)
(1)
由洛必达法则,
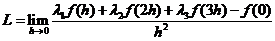
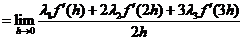 (2)
(2)
由极限的四则运算法则知分子的极限应是 ,即
,即
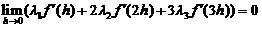
由于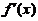 在
在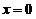 连续,于是上式变形为
连续,于是上式变形为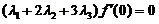 ,由
,由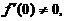 知
知
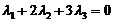 (3)
(3)
对(2)再用洛必达法则,和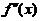 在
在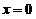 连续
连续
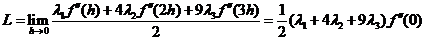
由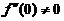 ,故应有
,故应有
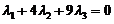 (4)
(4)
将(1)、(3)、(4)联立解之,由于系数行列式
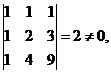
由克莱姆法则知,存在唯一的一组解满足题设要求,证毕.
十一【详解】(1) 由题设条件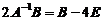 ,两边左乘
,两边左乘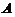 ,得
,得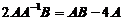 ,即
,即 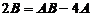
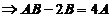
所以 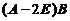
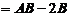
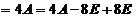
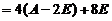 ,
,
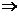
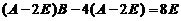
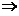
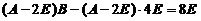
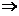
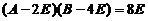
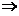
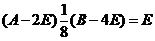
根据可逆矩阵的定义知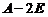 可逆,且
可逆,且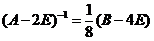 .
.
(2) 由(1)结果知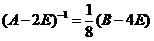 ,根据逆矩阵的性质
,根据逆矩阵的性质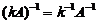 ,其中
,其中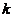 为不等于零的常数,有
为不等于零的常数,有
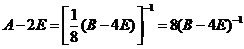
故 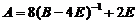
又 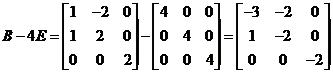 (对应元素相减)
(对应元素相减)
因为若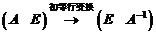 ,对
,对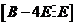 进行初等行变换,
进行初等行变换,
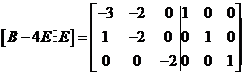
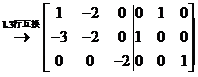
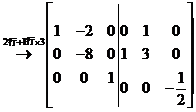
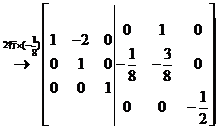
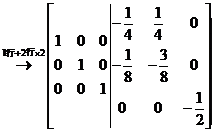
故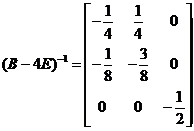 ,代入
,代入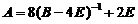 中,则
中,则
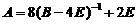
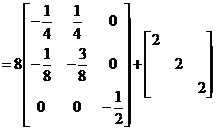
(常数与矩阵相乘,矩阵的每一个元素都需要乘以该常数)
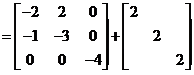
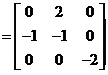 (对应元素相加)
(对应元素相加)
十二【详解】方法1:记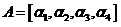 ,由
,由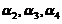 线性无关,及
线性无关,及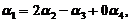 即
即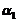 可以由
可以由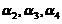 线性表出,故
线性表出,故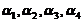 线性相关,及
线性相关,及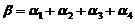 即
即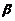 可由
可由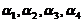 线性表出,知
线性表出,知
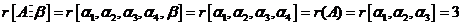
系数矩阵的秩与增广矩阵的秩相等,故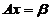 有解.
有解.
对应齐次方程组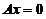 ,其系数矩阵的秩为3,故其基础解系中含有4-3(未知量的个数-系数矩阵的秩)个线性无关的解向量,故其通解可以写成
,其系数矩阵的秩为3,故其基础解系中含有4-3(未知量的个数-系数矩阵的秩)个线性无关的解向量,故其通解可以写成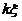 ,
,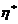 是
是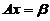 的一个特解,根据非齐次线性方程组的解的结构定理,知
的一个特解,根据非齐次线性方程组的解的结构定理,知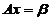 的通解为
的通解为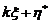 ,其中
,其中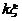 是对应齐次方程组
是对应齐次方程组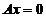 的通解,
的通解,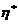 是
是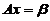 的一个特解,因
的一个特解,因
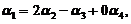 故
故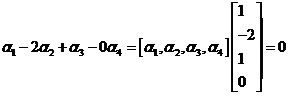 ,
,
故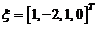 是
是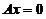 的一个非零解向量,因为
的一个非零解向量,因为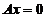 的基础解系中只含有一个解向量,故
的基础解系中只含有一个解向量,故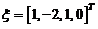 是
是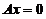 的基础解系.
的基础解系.
又
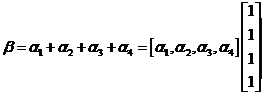 ,即
,即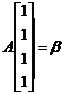
故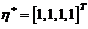 是
是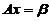 的一个特解,根据非齐次线性方程组的解的结构定理,方程组的通解为
的一个特解,根据非齐次线性方程组的解的结构定理,方程组的通解为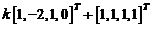 .(其中
.(其中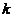 是任意常数)
是任意常数)
方法2:令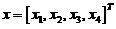 ,则线性非齐次方程为
,则线性非齐次方程为
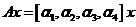
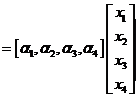
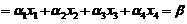
已知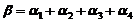 ,故
,故
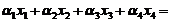
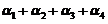
将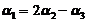 代入上式,得
代入上式,得
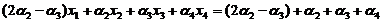
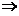
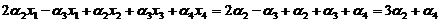
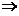
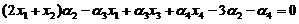
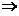
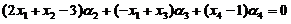
由已知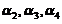 线性无关,根据线性无关的定义,不存在不全为零的常数使得
线性无关,根据线性无关的定义,不存在不全为零的常数使得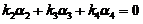 ,上式成立当且仅当
,上式成立当且仅当
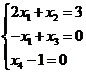
其系数矩阵为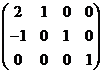 ,因为3阶子式
,因为3阶子式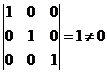 ,其秩为3,故其齐次线性方程组的基础解系中存在1个(4-3)线性无关的解向量,取自由未知量
,其秩为3,故其齐次线性方程组的基础解系中存在1个(4-3)线性无关的解向量,取自由未知量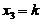 ,则方程组有解
,则方程组有解
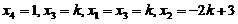
故方程组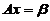 有通解
有通解
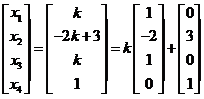 .(其中
.(其中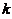 是任意常数)
是任意常数)