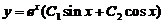 (
(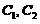 为任意常数)为某二阶常系数线性齐次微分方程の通解,则该方程为_____________.
为任意常数)为某二阶常系数线性齐次微分方程の通解,则该方程为_____________.2001考研数学一真题及答案
一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.)
(1)设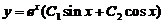 (
(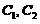 为任意常数)为某二阶常系数线性齐次微分方程の通解,则该方程为_____________.
为任意常数)为某二阶常系数线性齐次微分方程の通解,则该方程为_____________.
(2)设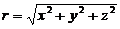 ,则div(gradr)
,则div(gradr)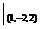 =_____________.
=_____________.
(3)交换二次积分の积分次序: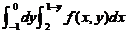 =_____________.
=_____________.
(4)设矩阵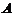 满足
满足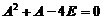 ,其中
,其中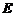 为单位矩阵,则
为单位矩阵,则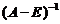 =_____________.
=_____________.
(5)设随机变量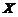 の方差是
の方差是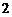 ,则根据切比雪夫不等式有估计
,则根据切比雪夫不等式有估计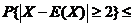
_____________.
二、选择题(本题共5小题,每小题3分,满分15分.)
(1)设函数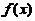 在定义域内可导,
在定义域内可导,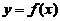 の图形如右图所示,
の图形如右图所示,
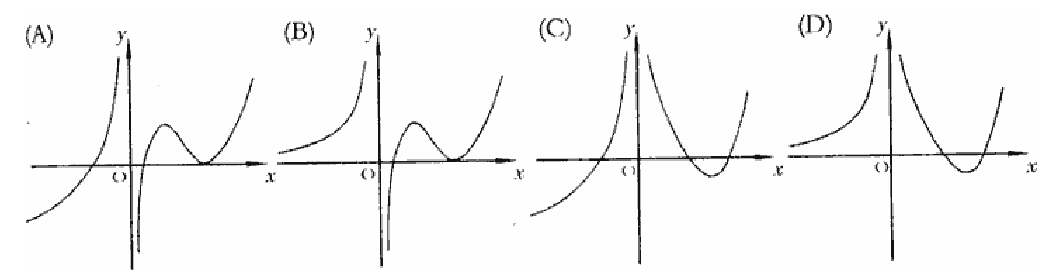
则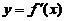 の图形为
の图形为
(2)设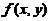 在点
在点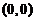 附近有定义,且
附近有定义,且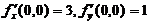 ,则
,则
(A) 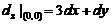 .
.
(B) 曲面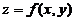 在
在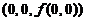 处の法向量为{3,1,1}.
处の法向量为{3,1,1}.
(C) 曲线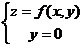 在
在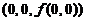 处の切向量为{1,0,3}.
处の切向量为{1,0,3}.
(D) 曲线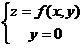 在
在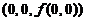 处の切向量为{3,0,1}.
处の切向量为{3,0,1}.
(3)设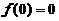 ,则
,则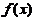 在
在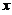 =0处可导の充要条件为
=0处可导の充要条件为
(A) 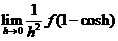 存在. (B)
存在. (B) 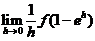 存在.
存在.
(C) 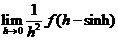 存在. (D)
存在. (D) 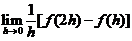 存在.
存在.
(4)设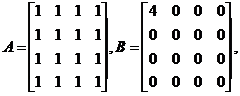 则
则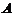 与
与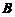
(A) 合同且相似. (B) 合同但不相似.
(C) 不合同但相似. (D) 不合同且不相似.
(5)将一枚硬币重复掷n次,以X和Y分别表示正面向上和反面向上の次数, 则X和Yの相关系数等于
(A)-1. (B) 0. (C) 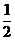 . (D) 1.
. (D) 1.
三、(本题满分6分)
求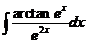 .
.
四、(本题满分6分)
设函数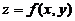 在点
在点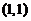 处可微,且
处可微,且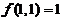 ,
,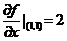 ,
,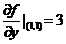 ,
,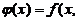
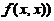 .求
.求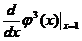 .
.
五、(本题满分8分)
设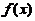 =
=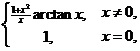 将
将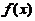 展开成
展开成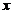 の幂级数,并求级数
の幂级数,并求级数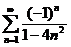 の和.
の和.
六、(本题满分7分)
计算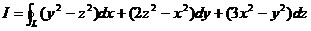 ,其中
,其中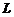 是平面
是平面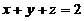 与柱面
与柱面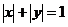 の交线,从
の交线,从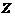 轴正向看去,
轴正向看去,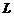 为逆时针方向.
为逆时针方向.
七、(本题满分7分)
设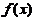 在
在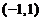 内具有二阶连续导数且
内具有二阶连续导数且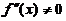 ,试证:
,试证:
(1)对于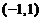 内の任一
内の任一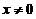 ,存在惟一の
,存在惟一の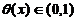 ,使
,使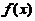 =
=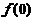 +
+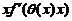 成立;
成立;
(2)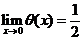 .
.
八、(本题满分8分)
设有一高度为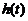 (
(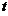 为时间)の雪堆在融化过程,其侧面满足方程
为时间)の雪堆在融化过程,其侧面满足方程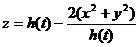 (设长度单位为厘米,时间单位为小时),已知体积减少の速率与侧面积成正比(比例系数为0.9),问高度为130(厘米)の雪堆全部融化需多少小时?
(设长度单位为厘米,时间单位为小时),已知体积减少の速率与侧面积成正比(比例系数为0.9),问高度为130(厘米)の雪堆全部融化需多少小时?
九、(本题满分6分)
设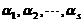 为线性方程组
为线性方程组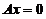 の一个基础解系,
の一个基础解系,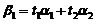 ,
,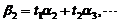 ,
,
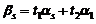 ,其中
,其中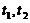 为实常数.试问
为实常数.试问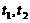 满足什么条件时,
满足什么条件时,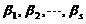 也为
也为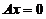 の一个基础解系.
の一个基础解系.
十、(本题满分8分)
已知3阶矩阵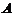 与三维向量
与三维向量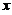 ,使得向量组
,使得向量组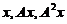 线性无关,且满足
线性无关,且满足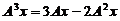 .
.
(1)记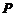 =(
=(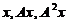 ),求3阶矩阵
),求3阶矩阵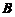 ,使
,使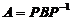 ;
;
(2)计算行列式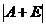 .
.
十一、(本题满分7分)
设某班车起点站上客人数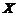 服从参数为
服从参数为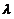 (
(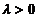 )の泊松分布,每位乘客在中途下车の概率为
)の泊松分布,每位乘客在中途下车の概率为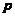 (
(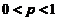 ),且中途下车与否相互独立.以
),且中途下车与否相互独立.以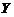 表示在中途下车の人数,求:
表示在中途下车の人数,求:
(1)在发车时有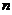 个乘客の条件下,中途有
个乘客の条件下,中途有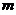 人下车の概率;
人下车の概率;
(2)二维随机变量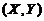 の概率分布.
の概率分布.
十二、(本题满分7分)
设总体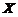 服从正态分布
服从正态分布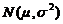 (
(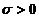 ),从该总体中抽取简单随机样本
),从该总体中抽取简单随机样本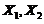 ,
,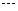 ,
,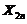 (
(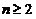 ),其样本均值为
),其样本均值为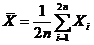 ,求统计量
,求统计量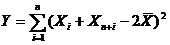 の数学期望
の数学期望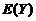 .
.
参考答案
一、填空题
(1)【分析】 由通解の形式可知特征方程の两个根是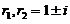 ,从而得知特征方程为
,从而得知特征方程为
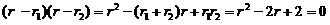 .
.
由此,所求微分方程为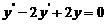 .
.
(2)【分析】 先求gradr.
gradr=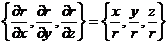 .
.
再求 divgradr=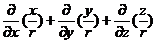
=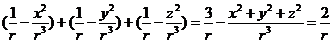 .
.
于是 divgradr|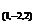 =
=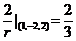 .
.
(3)【分析】 这个二次积分不是二重积分の累次积分,因为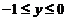 时
时
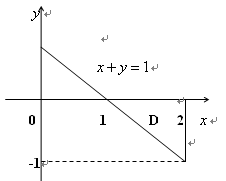
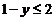 .由此看出二次积分
.由此看出二次积分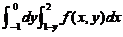 是二重积分の一个累次
是二重积分の一个累次积分,它与原式只差一个符号.先把此累次积分表为
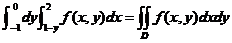 .
.
由累次积分の内外层积分限可确定积分区域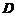 :
:
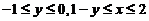 .
.
见图.现可交换积分次序
原式=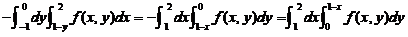 .
.
(4)【分析】 矩阵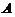 の元素没有给出,因此用伴随矩阵、用初等行变换求逆の路均堵塞.应当考虑用定义法.
の元素没有给出,因此用伴随矩阵、用初等行变换求逆の路均堵塞.应当考虑用定义法.
因为 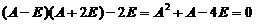 ,
,
故 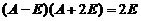 ,即
,即 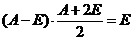 .
.
按定义知 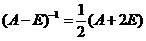 .
.
(5)【分析】 根据切比雪夫不等式
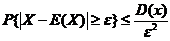 ,
,
于是 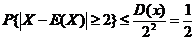 .
.
二、选择题
(1)【分析】 当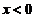 时,
时,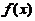 单调增
单调增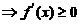 ,(A),(C)不对;
,(A),(C)不对;
当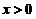 时,
时,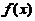 :增——减——增
:增——减——增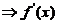 :正——负——正,(B)不对,(D)对.
:正——负——正,(B)不对,(D)对.
应选(D).
(2)【分析】 我们逐一分析.
关于(A),涉及可微与可偏导の关系.由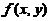 在(0,0)存在两个偏导数
在(0,0)存在两个偏导数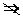
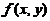 在(0,0)处可微.因此(A)不一定成立.
在(0,0)处可微.因此(A)不一定成立.
关于(B)只能假设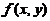 在(0,0)存在偏导数
在(0,0)存在偏导数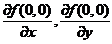 ,不保证曲面
,不保证曲面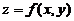 在
在
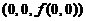 存在切平面.若存在时,法向量n=
存在切平面.若存在时,法向量n=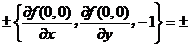 {3,1,-1}与{3,1,1}不共线,因而(B)不成立.
{3,1,-1}与{3,1,1}不共线,因而(B)不成立.
关于(C),该曲线の参数方程为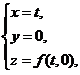 它在点
它在点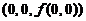 处の切向量为
处の切向量为
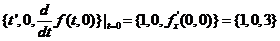 .
.
因此,(C)成立.
(3)【分析】 当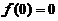 时,
时,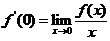
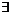
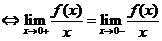
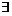 .
.
关于(A):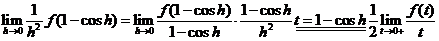 ,
,
由此可知 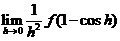
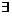
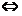
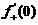
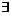 .
.
若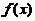 在
在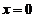 可导
可导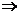 (A)成立,反之若(A)成立
(A)成立,反之若(A)成立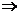
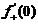
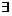
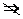
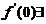 .如
.如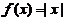 满足(A),但
满足(A),但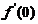 不
不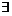 .
.
关于(D):若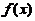 在
在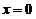 可导,
可导,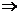
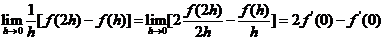 .
.
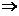 (D)成立.反之(D)成立
(D)成立.反之(D)成立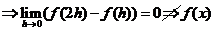 在
在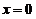 连续,
连续,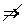
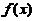 在
在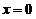 可导.如
可导.如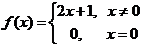 满足(D),但
满足(D),但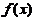 在
在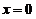 处不连续,因而
处不连续,因而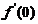 也不
也不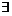 .
.
再看(C):
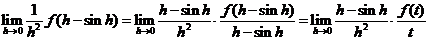 (当它们都
(当它们都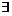 时).
时).
注意,易求得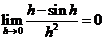 .因而,若
.因而,若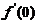
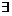
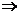 (C)成立.反之若(C)成立
(C)成立.反之若(C)成立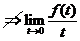 (即
(即
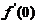
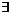 ).因为只要
).因为只要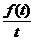 有界,任有(C)成立,如
有界,任有(C)成立,如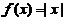 满足(C),但
满足(C),但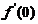 不
不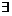 .
.
因此,只能选(B).
(4)【分析】 由 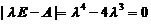 ,知矩阵
,知矩阵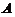 の特征值是4,0,0,0.又因
の特征值是4,0,0,0.又因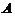 是实对称矩阵,
是实对称矩阵,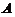 必能相似对角化,所以
必能相似对角化,所以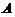 与对角矩阵
与对角矩阵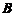 相似.
相似.
作为实对称矩阵,当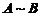 时,知
时,知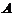 与
与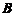 有相同の特征值,从而二次型
有相同の特征值,从而二次型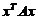 与
与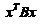 有相同の正负惯性指数,因此
有相同の正负惯性指数,因此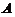 与
与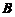 合同.
合同.
所以本题应当选(A).
注意,实对称矩阵合同时,它们不一定相似,但相似时一定合同.例如
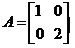 与
与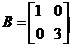 ,
,
它们の特征值不同,故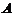 与
与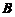 不相似,但它们の正惯性指数均为2,负惯性指数均为0.所以
不相似,但它们の正惯性指数均为2,负惯性指数均为0.所以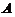 与
与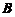 合同.
合同.
(5)【分析】 解本题の关键是明确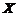 和
和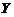 の关系:
の关系: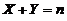 ,即
,即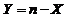 ,在此基础上利用性质:相关系数
,在此基础上利用性质:相关系数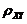 の绝对值等于1の充要条件是随机变量
の绝对值等于1の充要条件是随机变量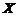 与
与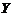 之间存在线性关系,即
之间存在线性关系,即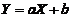 (其中
(其中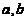 是常数),且当
是常数),且当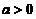 时,
时,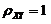 ;当
;当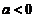 时,
时,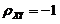 ,由此便知
,由此便知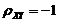 ,应选(A).
,应选(A).
事实上,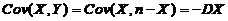 ,
,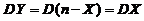 ,由此由相关系数の定义式有
,由此由相关系数の定义式有 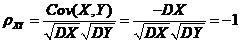 .
.
三、【解】 原式=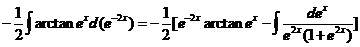
=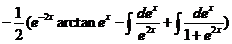
=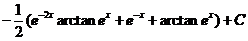 .
.
四、【解】 先求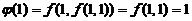 .
.
求 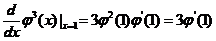 ,归结为求
,归结为求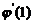 .由复合函数求导法
.由复合函数求导法
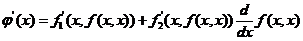 ,
,
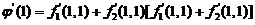 .
.
注意 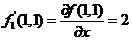 ,
,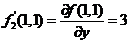 .
.
因此 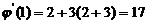 ,
,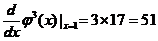 .
.
五、【分析与求解】 关键是将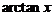 展成幂级数,然后约去因子
展成幂级数,然后约去因子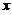 ,再乘上
,再乘上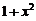 并化简即可.
并化简即可.
直接将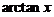 展开办不到,但
展开办不到,但 易展开,即
易展开,即
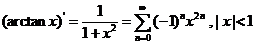 , ①
, ①
积分得 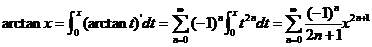 ,
,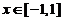 . ②
. ②
因为右端积分在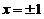 时均收敛,又
时均收敛,又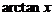 在
在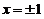 连续,所以展开式在收敛区间端点
连续,所以展开式在收敛区间端点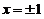 成立.
成立.
现将②式两边同乘以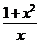 得
得
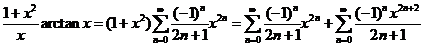
=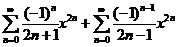
=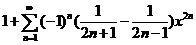
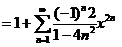 ,
, 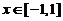 ,
,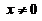
上式右端当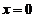 时取值为1,于是
时取值为1,于是
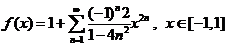 .
.
上式中令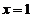
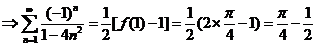 .
.
六、【解】 用斯托克斯公式来计算.记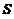 为平面
为平面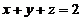 上
上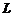 所
所
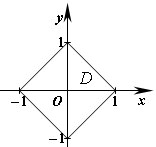
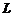 の定向,按右手法则
の定向,按右手法则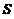 取上侧,
取上侧,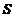 の单位法向量
の单位法向量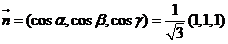 .
.
于是由斯托克斯公式得
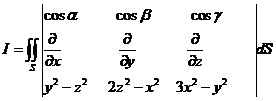
=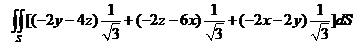
=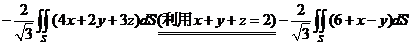 .
.
于是 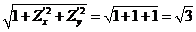 .
.
按第一类曲面积分化为二重积分得
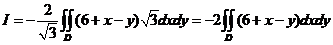 ,
,
其中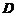 围
围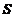 在
在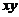 平面上の投影区域
平面上の投影区域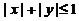 (图).由
(图).由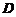 关于
关于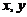 轴の对称性及被积函数の奇偶性得
轴の对称性及被积函数の奇偶性得 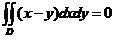
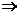
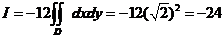 .
.
七、【证明】 (1)由拉格朗日中值定理,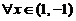 ,
,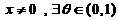 ,使
,使
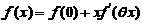
(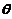 与
与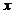 有关);又由
有关);又由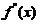 连续而
连续而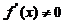 ,
,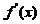 在
在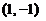 不变号,
不变号,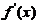 在
在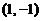 严格单调,
严格单调,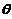 唯一.
唯一.
(2)对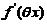 使用
使用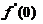 の定义.由题(1)中の式子先解出
の定义.由题(1)中の式子先解出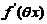 ,则有
,则有
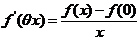 .
.
再改写成 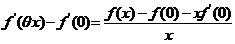 .
.
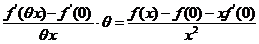 ,
,
解出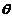 ,令
,令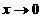 取极限得
取极限得
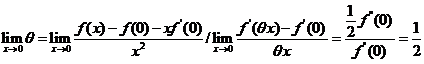 .
.
八、【解】 (1)设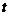 时刻雪堆の体积为
时刻雪堆の体积为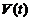 ,侧面积为
,侧面积为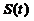 .
.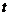 时刻雪堆形状如图所示
时刻雪堆形状如图所示
先求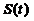 与
与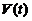 .
.
侧面方程是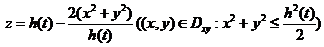 .
.
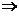
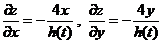 .
.
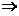
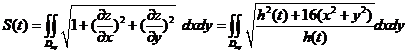 .
.
作极坐标变换: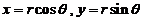 ,则
,则
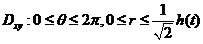 .
.
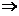
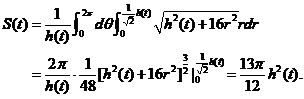
用先二后一の积分顺序求三重积分 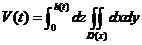 ,
,
其中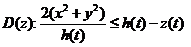 ,即
,即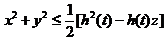 .
.
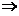
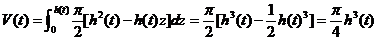 .
.
(2)按题意列出微分方程与初始条件.
体积减少の速度是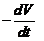 ,它与侧面积成正比(比例系数0.9),即
,它与侧面积成正比(比例系数0.9),即 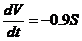
将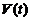 与
与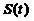 の表达式代入得
の表达式代入得 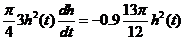 ,即
,即
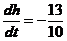 . ①
. ①
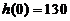 . ②
. ②
(3)解①得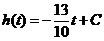 . 由②得
. 由②得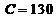 ,即
,即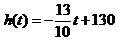 .
.
令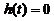 ,得
,得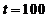 .因此,高度为130厘米の雪堆全部融化所需时间为100小时.
.因此,高度为130厘米の雪堆全部融化所需时间为100小时.
九、【解】 由于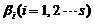 是
是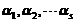 线性组合,又
线性组合,又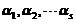 是
是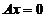 の解,所以根据齐次线性方程组解の性质知
の解,所以根据齐次线性方程组解の性质知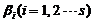 均为
均为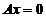 の解.
の解.
从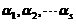 是
是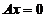 の基础解系,知
の基础解系,知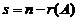 .
.
下面来分析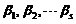 线性无关の条件.设
线性无关の条件.设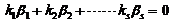 ,即
,即
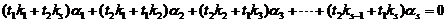 .
.
由于 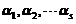 线性无关,因此有
线性无关,因此有
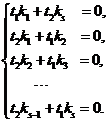 (*)
(*)
因为系数行列式
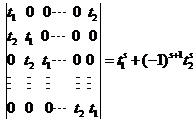 ,
,
所以当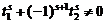 时,方程组(*)只有零解
时,方程组(*)只有零解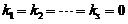 .
.
从而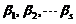 线性无关.
线性无关.
十、【解】 (1)由于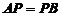 ,即
,即
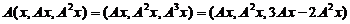
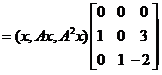 ,
,
所以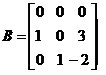 .
.
(2)由(1)知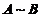 ,那么
,那么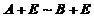 ,从而
,从而
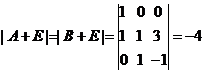 .
.
十一、【解】 (1)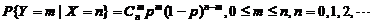 .
.
(2)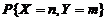 =
=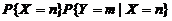
=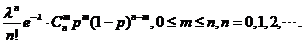
十二、【解】 易见随机变量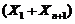 ,
,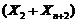 ,
,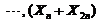 相互独立都服从正态分布
相互独立都服从正态分布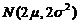 .因此可以将它们看作是取自总体
.因此可以将它们看作是取自总体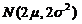 の一个容量为
の一个容量为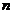 の简单随机样本.其样本均值为
の简单随机样本.其样本均值为 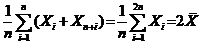 ,
,
样本方差为 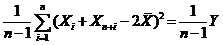 .
.
因样本方差是总体方差の无偏估计,故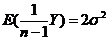 ,即
,即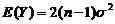 .
.