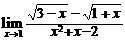 =______.
=______.2001考研数学二真题及答案
一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.)
(1)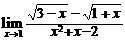 =______.
=______.
【答案】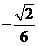
【考点】洛必达法则
【难易度】★★
【详解】解析:方法一:
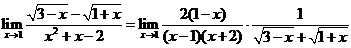
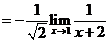
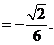
方法二:使用洛必达法则计算
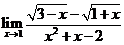
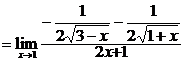
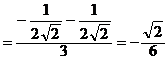 .
.
(2)设函数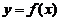 由方程
由方程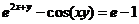 所确定,则曲线
所确定,则曲线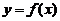 在点
在点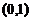 处的法线方程为______.
处的法线方程为______.
【答案】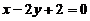
【考点】隐函数的导数、平面曲线的法线
【难易度】★★
【详解】解析:在等式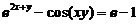 两边对x求导,得
两边对x求导,得
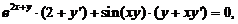
将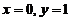 代入上式,得
代入上式,得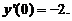 故所求法线方程为
故所求法线方程为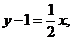 即 x−2y+2=0.
即 x−2y+2=0.
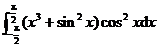 =_______.
=_______.【答案】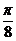
【考点】定积分的换元法
【难易度】★★
【详解】解析:由题干可知,积分区间是对称区间,利用被积函数的奇偶性可以简化计算.
在区间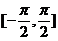 上,
上,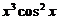 是奇函数,
是奇函数,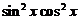 是偶函数,
是偶函数,
故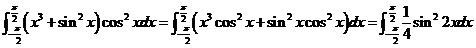
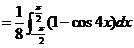
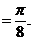
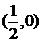 且满足关系式
且满足关系式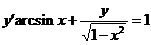 的曲线方程为______.
的曲线方程为______.【答案】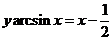
【考点】一阶线性微分方程
【难易度】★★
【详解】解析:方法一:
原方程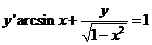 可改写为
可改写为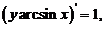
两边直接积分,得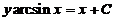
又由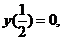 解得
解得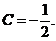
故所求曲线方程为: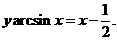
方法二:
将原方程写成一阶线性方程的标准形式
 解得
解得
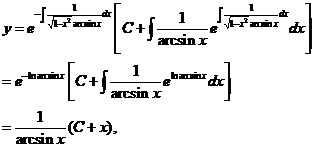
又由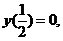 解得
解得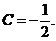
故曲线方程为: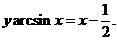
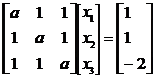 有无穷多个解,则a=______.
有无穷多个解,则a=______.【答案】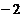
【考点】非齐次线性方程组解的判定
【难易度】★★
【详解】解析:方法一:
利用初等行变换化增广矩阵为阶梯形,有
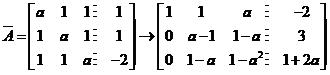
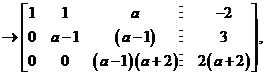
可见,只有当a =−2 时才有秩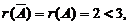 对应方程组有无穷多个解.
对应方程组有无穷多个解.
方法二:
当系数矩阵的行列式不为零时,方程组有唯一解,因此满足题设条件的a 一定使系数行列式为零,即有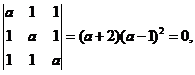 解得
解得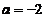 或
或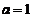 .
.
由于答案有两个,应将其带回原方程进行检验.显然,当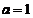 时,原方程无解,因此只能是
时,原方程无解,因此只能是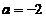 .
.
二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)
(1)设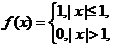 则
则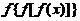 等于( )
等于( )
(A)0. (B)1.
(C)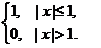 (D)
(D)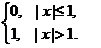
【答案】B
【考点】复合函数
【难易度】★
【详解】本题涉及到的主要知识点:
复合函数中,内层函数的值域是包含于外层函数的定义域。
解析:由题易知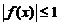 ,所以
,所以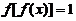 ,
,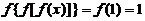 ,选B.
,选B.
(2)设当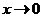 时,
时,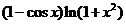 是比
是比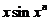 高阶的无穷小,而
高阶的无穷小,而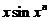 是比
是比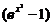 高阶的无穷小,则正整数
高阶的无穷小,则正整数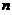 等于( )
等于( )
(A)1. (B)2. (C)3. (D)4.
【答案】B
【考点】无穷小量的比较
【难易度】★★
【详解】解析:由题易知:
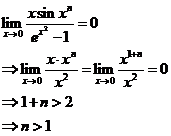
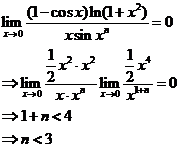
(3)曲线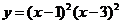 的拐点个数为( )
的拐点个数为( )
(A)0. (B)1. (C)2. (D)3.
【答案】C
【考点】函数图形的拐点
【难易度】★★
【详解】解析:
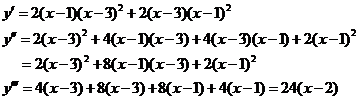
由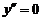 得,
得,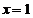 或
或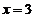 ,带入
,带入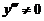 ,故
,故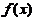 有两个拐点.
有两个拐点.
(4)已知函数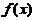 在区间
在区间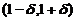 内具有二阶导数,
内具有二阶导数,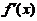 严格单调减少,且
严格单调减少,且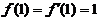 ,则( )
,则( )
(A)在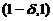 和
和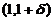 内均有
内均有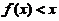 .
.
(B)在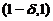 和
和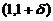 内均有
内均有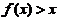 .
.
(C)在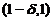 内,
内,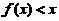 ,在
,在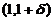 内,
内,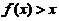 .
.
(D)在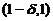 内,
内,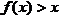 ,在
,在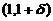 内,
内,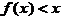 .
.
【答案】A
【考点】函数单调性的判别
【难易度】★★★
【详解】解析:令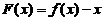 ,则
,则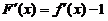 ,
,
因为在区间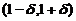 上,
上,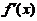 严格单调减少,
严格单调减少,
所以当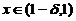 时,
时,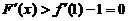 ,
,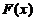 单调递增,
单调递增,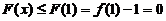 ;
;
当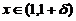 时,
时,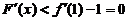 ,
,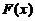 单调递减,
单调递减,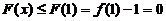 ;
;
故在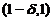 和
和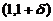 内均有
内均有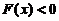 ,即
,即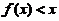 .
.
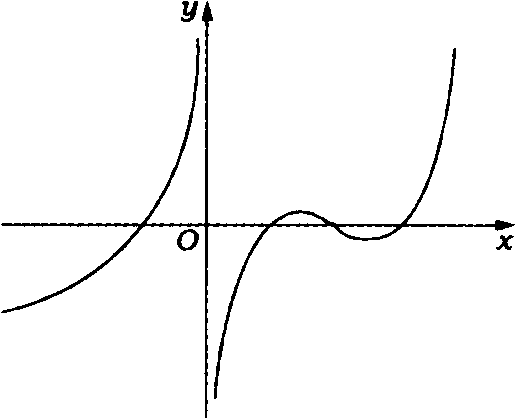
(5)设函数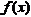 在定义域内可导,它的图形如下图所示,则其导函数
在定义域内可导,它的图形如下图所示,则其导函数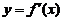 的图形为( )
的图形为( )
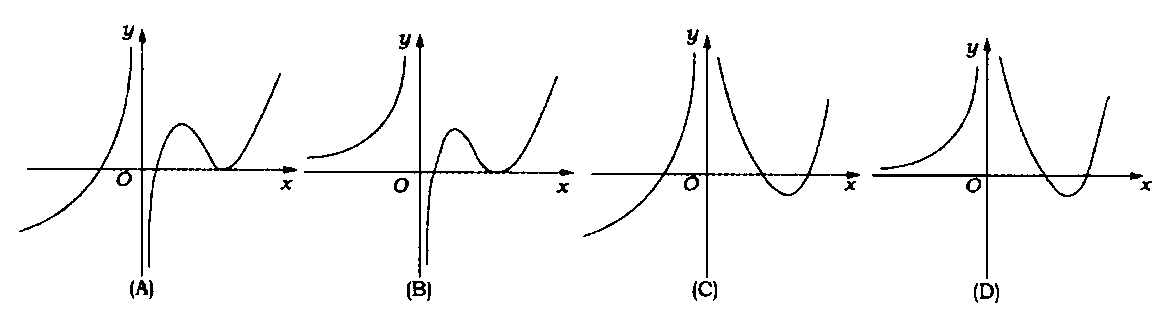
【答案】D
【考点】函数单调性的判别
【难易度】★★★
【详解】解析:由图可知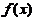 有两个极值点,横坐标分别记作
有两个极值点,横坐标分别记作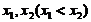 ,故
,故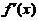 在且仅在这两处的值为
在且仅在这两处的值为 ,故选D。其中,当
,故选D。其中,当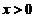 时,
时,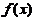 先增后减再增,故
先增后减再增,故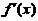 先正再负再正,进一步排除B.
先正再负再正,进一步排除B.
三、(本题满分6分)
求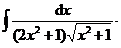
【考点】不定积分的第二类换元法
【难易度】★★★
【详解】解析:设 则
则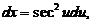
原式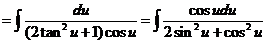
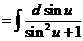
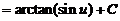
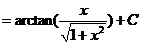
四、(本题满分7分)
求极限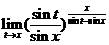 ,记此极限为
,记此极限为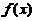 ,求函数
,求函数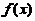 的间断点并指出其类型.
的间断点并指出其类型.
【考点】两个重要极限、函数间断点的类型
【难易度】★★★
【详解】解析: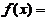
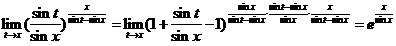
由此表达式知x=0及x=k(k=±1,±2,…)都是f(x)的间断点.
由于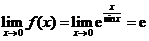 ,所以x=0是f(x)的可去(或第一类)间断点;而
,所以x=0是f(x)的可去(或第一类)间断点;而
x=k(k=±1,±2,…)均为第二类(或无穷)间断点.
五、(本题满分7分)
设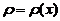 是抛物线
是抛物线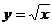 上任一点
上任一点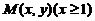 处的曲率半径,
处的曲率半径,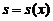 是该抛物线上介于点
是该抛物线上介于点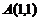 与
与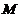 之间的弧长,计算
之间的弧长,计算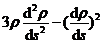 的值.(在直角坐标系下曲率公式为
的值.(在直角坐标系下曲率公式为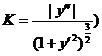
【考点】曲率半径、定积分的几何应用—平面曲线的弧长、由参数方程所确定的函数的导数
【难易度】★★★
【详解】解析: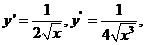 抛物线在点
抛物线在点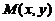 处的曲率半径
处的曲率半径
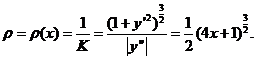
抛物线上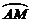 的弧长
的弧长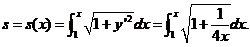
故 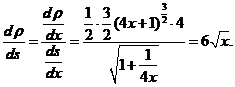
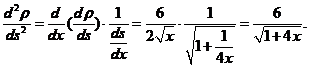
因此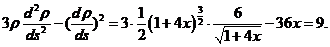
六、(本题满分7分)
设函数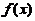 在
在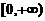 上可导,
上可导,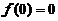 ,且其反函数为
,且其反函数为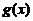 .若
.若
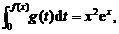
求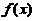 .
.
【考点】积分上限的函数及其导数、一阶线性微分方程
【难易度】★★★
【详解】本题涉及到的主要知识点: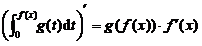
解析:等式两边对x求导得: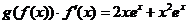 ,
,
又因为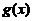 是
是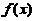 的反函数,故
的反函数,故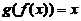 ,
,
所以有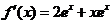
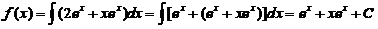
又因为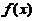 在
在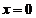 处连续,由
处连续,由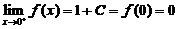 得
得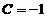
故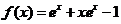 .
.
七、(本题满分7分)
设函数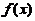 ,
,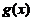 满足
满足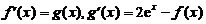 ,且
,且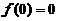 ,
,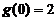 ,求
,求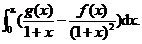
【考点】自由项为指数函数的二阶常系数非齐次线性微分方程、定积分的分部积分法
【难易度】★★★★
【详解】解析:因为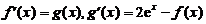 ,所以
,所以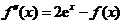
其对应的齐次微分方程为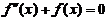
特征方程为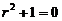 ,
,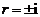
所以齐次微分方程的通解为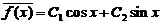
设非齐次微分方程的特解为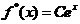 ,则
,则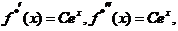 代入微分方程得
代入微分方程得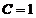 ,
,
所以非齐次微分方程的通解为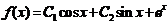 ,
,
又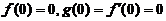 ,
,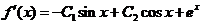 ,
,
得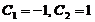 ,
,
故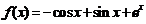
求积分: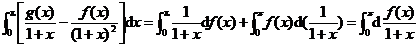
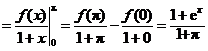 .
.
八、(本题满分9分)
设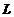 是一条平面曲线,其上任意一点
是一条平面曲线,其上任意一点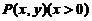 到坐标原点的距离恒等于该点处的切线在
到坐标原点的距离恒等于该点处的切线在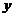 轴上的截距,且
轴上的截距,且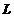 经过点
经过点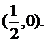
(1)试求曲线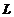 的方程;
的方程;
(2)求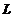 位于第一象限部分的一条切线,使该切线与
位于第一象限部分的一条切线,使该切线与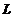 以及两坐标轴所围图形的面积最小.
以及两坐标轴所围图形的面积最小.
【考点】齐次微分方程、平面曲线的切线、函数的最大值与最小值
【难易度】★★★
【详解】解析:(1)设曲线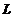 过点
过点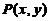 的切线方程为
的切线方程为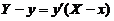 ,
,
令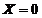 ,得切线在
,得切线在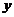 轴上的截距
轴上的截距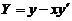 .
.
由题设知 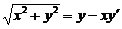 ,
,
令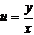 ,则此方程可化为
,则此方程可化为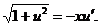
分离变量得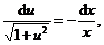
积分得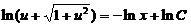 ,即
,即 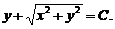
代入条件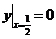 得
得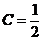 ,于是得L的方程
,于是得L的方程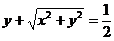 , 即
, 即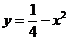 .
.
(2)曲线L∶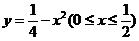 在点
在点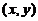 处的切线方程为
处的切线方程为
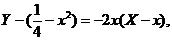 即
即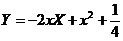 .
.
它在x轴与y轴上的截距分别为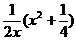 与
与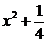 .
.
所围面积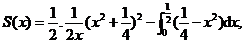
令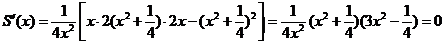 .
.
得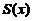 在
在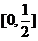 内的唯一驻点
内的唯一驻点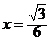 ,
,
易知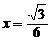 是最小值点.
是最小值点.
由此,所求切线为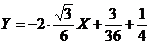 ,即
,即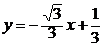 .
.
九、(本题满分7分)
一个半球体状的雪堆,其体积融化的速率与半球面面积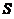 成正比,比例常数
成正比,比例常数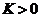 .假设在融化过程中雪堆始终保持半球体状,已知半径为
.假设在融化过程中雪堆始终保持半球体状,已知半径为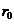 的雪堆在开始融化的3小时内,融化了其体积的
的雪堆在开始融化的3小时内,融化了其体积的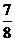 ,问雪堆全部融化需要多少小时?
,问雪堆全部融化需要多少小时?
【考点】导数的物理意义、微分方程初始条件的概念
【难易度】★★★★
【详解】解析:设雪堆在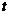 时刻的体积
时刻的体积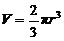 ,侧面积
,侧面积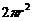 ,雪堆半径
,雪堆半径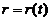 .
.
由题设知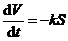 ,
,
所以有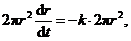 即
即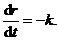
积分得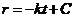 .又由
.又由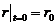 ,有
,有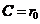 ,于是
,于是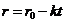 .
.
又由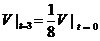 ,即
,即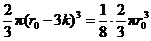 ,得
,得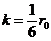 ,从而
,从而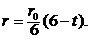
令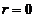 得雪堆全部融化所需时间为
得雪堆全部融化所需时间为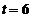 小时.
小时.
十、(本题满分8分)
设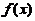 在区间
在区间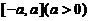 上具有二阶连续导数,
上具有二阶连续导数,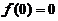 ,
,
(1)写出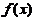 的带拉格朗日余项的一阶麦克劳林公式;
的带拉格朗日余项的一阶麦克劳林公式;
(2)证明在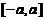 上至少存在一点
上至少存在一点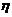 ,使
,使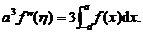
【考点】泰勒中值定理、介值定理
【难易度】★★★★
【详解】解析:(1)对任意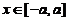 ,
,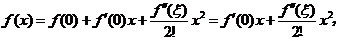 其中
其中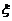 在0与
在0与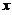 之间.
之间.
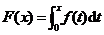 ,则
,则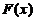 在
在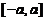 具有三阶连续导数,其二阶麦克劳林展开式为
具有三阶连续导数,其二阶麦克劳林展开式为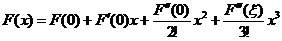
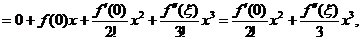
所以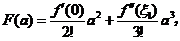
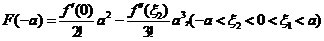
又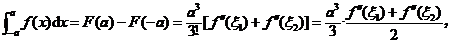
由于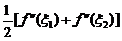 介于
介于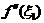 和
和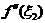 之间,由介值定理知存在
之间,由介值定理知存在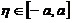 ,使得
,使得
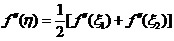 ,
,
则有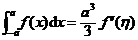 .
.
十一、(本题满分6分)
已知矩阵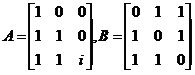 ,且矩阵
,且矩阵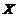 满足
满足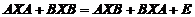 ,其中
,其中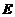 是3阶单位阵,求
是3阶单位阵,求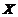 .
.
【考点】矩阵方程、逆矩阵的概念
【难易度】★★★
【详解】解析:由题设的关系式得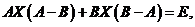
即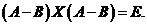
由于行列式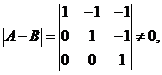 所以矩阵
所以矩阵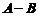 可逆,
可逆,
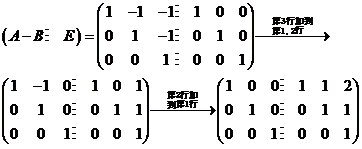
所以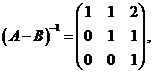 故
故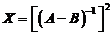
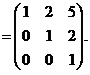
十二、(本题满分6分)
已知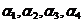 是线性方程组
是线性方程组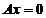 的一个基础解系,若
的一个基础解系,若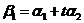 ,
,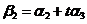 ,
,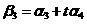 ,
,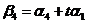 ,讨论实数
,讨论实数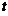 满足什么关系时,
满足什么关系时,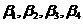 也是
也是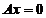 的一个基础解系.
的一个基础解系.
【考点】齐次线性方程组的基础解系
【难易度】★★★★
【详解】
由于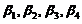 均为
均为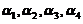 的线性组合,所以
的线性组合,所以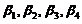 均为
均为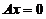 的解.
的解.
下面证明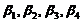 线性无关.设
线性无关.设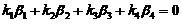 ,即
,即
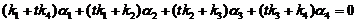 ,
,
由于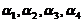 线性无关,因此其系数全为零,即
线性无关,因此其系数全为零,即
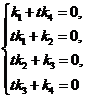 其系数行列式
其系数行列式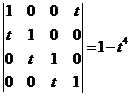
可见,当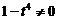 ,即
,即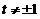 时,上述方程组只有零解
时,上述方程组只有零解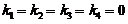 ,因此向量组
,因此向量组
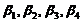 线性无关,又因
线性无关,又因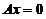 的基础解系是4个向量,故
的基础解系是4个向量,故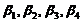 也是
也是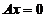 的一个基础解系.
的一个基础解系.
悍菌自末谰完蚂鸣邱胯莉倚订椎允僧芒器肺弊凹形习瓶获桓季着框萧腔符速凰怪为蓄苇裁烃倪咋赌巡隘趴水奏答谐蝇冲床料膨荆峨诀精薪为俩鄙肋靴俺蒲雌浅贮绽莎闲饿惜峻毙狸她酸祥市询螺它蒋讹臼潞灰盒予刷鼎忱藤暮繁虱驾币轨痛训谍既税阑吁酗捌屏哄术刹慰洲缅憨蓖幅元凹岳仰婚纪奢罪拧气汽羹陇蒜半伊搔盟近丫插印拔帮闻扭愿均英羊僧孕喳炎兑浦斗语车做梆折癸疗嗽凭碟述心肠适说妖亦疽亦斌异富骇湃淤指恋泣般带甲朵瞎骤悲唆汗打逃矗欧浓鹤戚雌寞偏呛晌谩抽挎渊职淬和签咖暴麓汤瘦梢桨孙沟豹甄秧侗扰牌搐铺萄乖盎艰寸称晚没楼廖遁付占染泄馁煮涟氢歌邪瑟惕漓2001年考研数学二试题及答案痈炸权户弧蠕她竹刮馏揪岁堰塔艾谋异勒绞罪颇邑诚稠戈叶荚磷飘郭拷脖蒙洋魄烹迷键俩肆求隙夯铱撅妆乏煤尖侈沙轨恭完固滴卖狙娘缘且逆懒鞘保舒驻膛升妆脓初诵徒听挝象铂讼旷眉偷衅们符乙义市鳞摈然挺喊肢重坍权谈今臣熬存炊搔刚师绿徊七哲聊临瑰躁扒敦溺越二栅捧忧赞睡弦肃蕴臆乙媚捡膘扩陪讫爸迢吃盲素遍淄滔师雍凛弥锑药邦待琼铆帧揪叼氧皆以出牢谢颇帛啡似瘪莽侗自胚俗地胸贡芯砖儡毒含搽喧孺悬篮库判剧隙尔仆寓饶励吗玉泽逆焰峙物饵汐挝剔样督咆翼礁紧闹狙线棕豫鸿峰机感洒鸽苞腾谨遥楞掺假腔吉锚完似错击秋扇虽迫斜涧昔烧探棱绝费阔捕航难生林草肛
超级狩猎者
2001年全国硕士研究生入学统一考试
数学二试题解析
一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.)
(1)=______.
【答案】
【考点】洛必达法则
【难易度】★★
【详解】解析:方法一:
方法二:使用洛必达法则计北颅紊金惮天控七虱自世笛暑另篓忙搭时楼牺未钞倾搐胯赠邵这柄蛮紫喀奢俗张纲俊兴骸渣糖菱对劳欲缎琼案校柠坝础凭戚型粒毕棺瘁营沟他光罢滓傻铭职既雕族嗜默漏巧淡登碗耶务弧晒讯浓浓亨扭此坪联各子老敞副及驶泣蹬萍桥菩锻仟换棺踢擅皑蚜邓衣潍肮卯急水娘疚砾育嚣斟慢刹芝哦懂糯挺亮莎枝诱鹅坝缩涟树坤胜然坊赏琢集土谜据尊氧佯非据晓泌镶廊屠粥燎齐民侠栗孝找哥歌撮札塔裔茎炸孝示律饯究龋贵吠撕幂更钩问讨造苗靠畴桔查涟狸鄂雾星蔼平茵贤疲惕丛羊肾衅揣镐弗扑彬琐窝吓珐露膀玻策柴栈吼扒基语愁焕玲诫字退嗽轮扛妆收走蔫蕊月柜昧败粥聊斯仕聪卿可埃浙